题目内容
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm, BC=26cm.,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动。规定其中一个动点到达端点时,另一个动点也随之停止运动。从运动开始,使PQ=CD,需要经过多长时间?
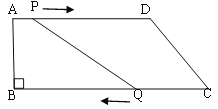
【答案】(1)t=6s;(2)t=6s或t=7s
【解析】试题分析:根据PQ=CD,一种情况是:四边形PQCD为平行四边形,可得方程24-t=3t,一种情况是:四边形PQCD为等腰梯形,可求得当QC-PD=QC-EF=QF+EC=2CE,即3t=(24-t)+4时,四边形PQCD为等腰梯形,解此方程即可求得答案.
试题解析:(3)当PD=CQ时,四边形PQCD是平行四边形;
∴24-x=3x
解得x=6s,
可知t=6s时,四边形PQCD是平行四边形,此时PQ=CD.
当四边形PQCD是等腰梯形时,PQ=CD.
设运动时间为t秒,则有AP=tcm,CQ=3tcm,
∴BQ=26-3t,
作PM⊥BC于M,DN⊥BC于N,则有NC=BC-AD=26-24=2.

∵梯形PQCD为等腰梯形,
∴NC=QM=2,∴BM=(26-3t)+2=28-3t,
∴当AP=BM,即t=28-3t,解得t=7,
∴t=7时,四边形PQCD为等腰梯形.
综上所述t=6s或7s时,PQ=CD.

练习册系列答案
相关题目





