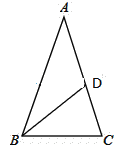
[题目]如图.△ABC中.∠A=36°.∠C=72°.∠DBC=36°.(1)求∠ABD的度数.(2)求证:BC=AD. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，△ABC中，∠A=36°，∠C=72°，∠DBC=36°.

（1）求∠ABD的度数。

（2）求证：BC=AD.

【答案】36°，∠C=∠BDC=72°

【解析】

（1）由∠C=72゜，∠A=∠DBC=36゜，根据三角形内角和定理，可求得∠ABD=∠A=36°；

（2）进一步求出∠ABC=∠BCD=∠BDC=72°，得出BD=BC，再由∠ABD=∠A得出BD=AD，继而求得答案．

（1）解：在△ABC中，

∠ABC=180°-∠A-∠C=72°，

∴∠ABD=∠ABC-∠DBC=36°；

（2）证明：在△BCD中，

∠BDC =180°-∠DBC-∠C=72°，

∴∠BDC =∠C，

∴BD=BC，

又∠ABD=∠A，

∴BD=AD，

∴BC=BD=AD，

∴BC= AD.

练习册系列答案

相关题目

【题目】如图（1），A1B1和A2B2是水面上相邻的两条赛道（看成两条互相平行的线段）．甲是一名游泳运动健将，乙是一名游泳爱好者，甲在赛道A1B1上从A1处出发，到达B1后，以同样的速度返回A1处，然后重复上述过程；乙在赛道A2B2上以1.5m/s的速度从B2处出发，到达A2后以相同的速度回到B2处，然后重复上述过程（不考虑每次折返时的减速和转向时间）．若甲、乙两人同时出发，设离开池边B1B2的距离为y（m），运动时间为t（s），甲游动时，y（m）与t（s）的函数图象如图2所示．
（1）赛道的长度是m，甲的速度是m/s；当t=s时，甲、乙两人第一次相遇，当t=s时，甲、乙两人第二次相遇？
（2）第三次相遇时，两人距池边B1B2多少米．

【题目】如图所示，△OAC和△BAD都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函数y= 在第一象限的图象经过点B，与OA交于点P，且OA2﹣AB2=18，则点P的横坐标为（）
A.9
B.6
C.3
D.3

【题目】如图，在矩形纸片ABCD中，AB＝4，BC＝6，将△ABC沿AC折叠，使点B落在点E处，CE交AD于点F，则DF的长等于(　　)

A. B. C. D.

【题目】放风筝是大家喜爱的一种运动，星期天的上午小明在市政府广场上放风筝．如图，他在A处不小心让风筝挂在了一棵树梢上，风筝固定在了D处，此时风筝AD与水平线的夹角为30°，为了便于观察，小明迅速向前边移动，收线到达了离A处10米的B处，此时风筝线BD与水平线的夹角为45°．已知点A，B，C在同一条水平直线上，请你求出小明此时所收回的风筝线的长度是多少米？（风筝线AD，BD均为线段， ≈1.414， ≈1.732，最后结果精确到1米）．

【题目】如图1，以边长为8的正方形纸片ABCD的边AB为直径作⊙O，交对角线AC于点E．
（1）线段AE=；
（2）如图2，以点A为端点作∠DAM=30°，交CD于点M，沿AM将四边形ABCM剪掉，使Rt△ADM绕点A逆时针旋转（如图3），设旋转角为α（0°＜α＜150°），旋转过程中AD与⊙O交于点F．
①当α=30°时，请求出线段AF的长；
②当α=60°时，求出线段AF的长；判断此时DM与⊙O的位置关系，并说明理由；
③当α= 时，DM与⊙O相切．