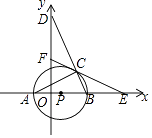题目内容
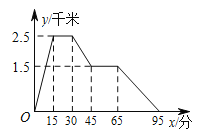
【题目】如图1,以边长为8的正方形纸片ABCD的边AB为直径作⊙O,交对角线AC于点E. 
(1)线段AE=;
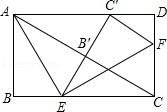
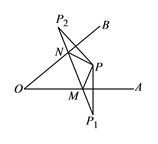
(2)如图2,以点A为端点作∠DAM=30°,交CD于点M,沿AM将四边形ABCM剪掉,使Rt△ADM绕点A逆时针旋转(如图3),设旋转角为α(0°<α<150°),旋转过程中AD与⊙O交于点F. 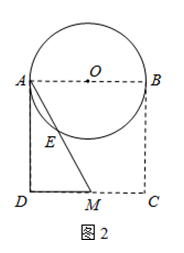
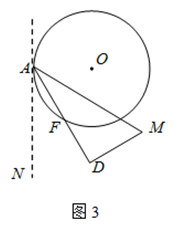
①当α=30°时,请求出线段AF的长;
②当α=60°时,求出线段AF的长;判断此时DM与⊙O的位置关系,并说明理由;
③当α= ![]() 时,DM与⊙O相切.
时,DM与⊙O相切.
【答案】
(1)4 ![]()
(2)解:①连接OA、OF,
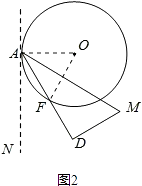
由题意得,∠NAD=30°,∠DAM=30°,
故可得∠OAM=30°,∠DAM=30°,
则∠OAF=60°,
又∵OA=OF,
∴△OAF是等边三角形,
∵OA=4,
∴AF=OA=4;
②连接B'F,此时∠NAD=60°,
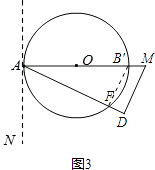
∵AB'=8,∠DAM=30°,
∴AF=AB'cos∠DAM=8× ![]() =4
=4 ![]() ;
;
此时DM与⊙O的位置关系是相离
③ 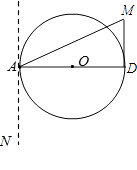
∵AD=8,直径的长度相等,
∴当DM与⊙O相切时,点D在⊙O上,
故此时可得α=∠NAD=90°.
【解析】解:(1)连接BE, 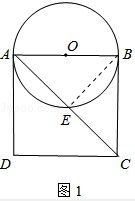
∵AC是正方形ABCD的对角线,
∴∠BAC=45°,
∴△AEB是等腰直角三角形,
又∵AB=8,
∴AE=4 ![]() ;
;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目