题目内容
【题目】如图是一个由5张纸片拼成的平行四边形，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为S1 ， 另两张直角三角形纸片的面积都为S2 ， 中间一张正方形纸片的面积为S3 ， 则这个平行四边形的面积一定可以表示为（ ）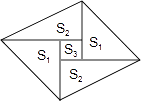 
A.4S1
B.4S2
C.4S2+S3
D.3S1+4S3
【答案】A
【解析】解：设等腰直角三角形的直角边为a，正方形边长为c， 则S2= 
（a+c）（a﹣c）= a2﹣ c2 ，
∴S2=S1﹣ S3 ，
∴S3=2S1﹣2S2 ，
∴平行四边形面积=2S1+2S2+S3=2S1+2S2+2S1﹣2S2=4S1 ．
故选A．
设等腰直角三角形的直角边为a，正方形边长为c，求出S2（用a、c表示），得出S1 ， S2 ， S3之间的关系，由此即可解决问题．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
