题目内容
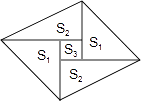
【题目】如图所示,在平行四边形ABCD中,∠ABE=∠AEB,AE∥DF,DC是∠ADF的角平分线.下列说法正确的是( )
①BE=CF ②AE是∠DAB的角平分线 ③∠DAE+∠DCF=120°.
A.①
B.①②
C.①②③
D.都不正确
【答案】C
【解析】解:∵四边形ABCD为平行四边形,
∴AD∥BC,且AD=BC,
又∵AE∥DF,
∴四边形AEDF为平行四边形,
∴EF=AD,
∴BC=EF,
∴BE=CF,
故①正确;
∵DC平分∠ADF,
∴∠ADC=∠FDC,
又∵AD∥EF,
∴∠ADC=∠DCF,
∴∠DCF=∠FDC,
∴DF=CF,
又∵AE=DF,
∴AE=CF=BE,
又∵∠ABE=∠AEB,
∴AB=AE,
∴△ABE和△CDF为等边三角形,
∴∠BAE=∠B=∠DAE=∠DCF=60°,
∴AE平分∠DAB,∠DAE+∠DCF=120°,
故②③正确;
故选C.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

练习册系列答案
相关题目