��Ŀ����
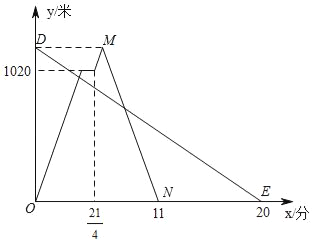
����Ŀ������������5�֣���ͼ��С���ڴ�¥30��
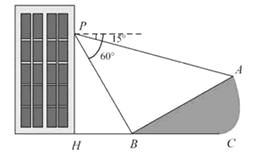
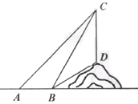
����PH��30�ף��Ĵ���P�����й۲⣬���ɽ
����A���ĸ���Ϊ15����ɽ��B���ĸ���Ϊ
60������֪��ɽ�µ��¶�i����tan��ABC��Ϊ1��
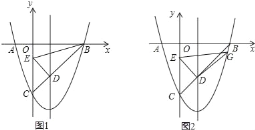
![]() ����P��H��B��C��A��ͬһ��ƽ���ϣ���
����P��H��B��C��A��ͬһ��ƽ���ϣ���
H��B��C��ͬһ��ֱ���ϣ���PH��HC��
(1)ɽ���½ǣ�����ABC���Ķ������� �� �ȣ�
(2)��A��B�����ľ��루�����ȷ��0.1�ף��ο����ݣ�![]() ��1.732����
��1.732����
���𰸡��⣺(1)30��
(2)�����P��ˮƽ��ΪPQ����������ã�![]()
![]() 450��
450��
![]()
![]()
![]()
![]()
![]()
![]()
![]() ��A��B�����ľ���Լ34.6�ס�
��A��B�����ľ���Լ34.6�ס�
��������
���⣨1�����ݸ����Լ��¶ȵĶ��弴����⣻
��2����ֱ����PHB�У��������Ǻ����������PB�ij���Ȼ����ֱ����PBA���������Ǻ���������⣮
���������
��1����ɽ�µ��¶�i����tan��ABC��Ϊ1��![]() ��
��
��tan��ABC=![]() ��
��
���ABC=30�㣻
�ߴ�P����ɽ��B���ĸ���60�㣬
���PBH=60�㣬
���ABP=180�㩁30�㩁60��=90��
�ʴ�Ϊ��90��
��2��������ã���PBH=60�㣬
�ߡ�ABC=30�㣬
���ABP=90�㣬
���PABΪֱ�������Σ�
�֡ߡ�APB=45�㣬
��ֱ����PHB�У�PB=PH��sin��PBH=45��![]() =30
=30![]() ��m����
��m����
��ֱ����PBA�У�AB=PBtan��BPA=30![]() ��52.0��m����
��52.0��m����
��A��B�����ľ���ԼΪ52.0�ף�