��Ŀ����
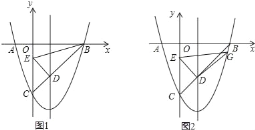
����Ŀ����ͼ����֪������y=x2��2x��3����x���ϵ�A��B���㣬��y�ύ�ڵ�C���߶�BC�������ߵĶԳ����ཻ�ڵ�D����EΪy���ϵ�һ�����㣮
��1����ֱ��BC�ĺ�������ʽ���������D�����ꣻ
��2�����E��������ΪΪm���ڵ�E���˶������У�����BDE��Ϊ�۽�������ʱ����m��ȡֵ��Χ��
��3����ͼ2������DE��������DE�Ƶ�D˳ʱ�뷽����ת90�����������߽���ΪG������EG��DG�õ�Rt��GED���ڵ�E���˶������У��Ƿ����������Rt��GED��ʹ����ֱ�DZ�֮��Ϊ2��1��������ڣ������ʱ��G�����ꣻ��������ڣ���˵�����ɣ�
���𰸡���1�� y=x��3��D������Ϊ��1����2������2�� m��3��m����1��m����3����3�����ڣ� G������Ϊ��1![]() ����3��0����1
����3��0����1![]() ����1��0����
����1��0����
��������
��1���ȸ�����������x��Ľ����������A����1��0����B��3��0�������öԳ��Կɵ������ߵĶԳ���Ϊֱ��x=1�������C��0����3����Ȼ�����ô���ϵ������ֱ��BC�Ľ���ʽ����x=1ʱ��y=x��3=��2����D������Ϊ��1����2����
��2����ͼ1�����жϡ�OBCΪ����ֱ�������Σ����OCB=��OBC=45�㣬�ټ����CD![]() ��Ȼ��ͨ�������BDEΪֱ��������ʱm��ֵ��ȷ����BDEΪ�۽�������ʱm��ȡֵ��Χ��
��Ȼ��ͨ�������BDEΪֱ��������ʱm��ֵ��ȷ����BDEΪ�۽�������ʱm��ȡֵ��Χ��
��3���������ۣ��ٵ���G�ڶԳ����Ҳ����������ʱ����ͼ2����DF��y����F��GH��DF��H����G��t��t2��2t��3������GH=t2��2t��3������2��=t2��2t��1������ת�����ʵá�EDG=90�㣬����֤��Rt��EDF��Rt��DGH���������Ƶ����ʵ�![]() ����
����![]() 2��
2��![]() ���з������t��ֵ���������G�����ꣻ�ڵ���G�ڶԳ���������������ʱ����ͬ���ķ����ɵ�G�����꣮
���з������t��ֵ���������G�����ꣻ�ڵ���G�ڶԳ���������������ʱ����ͬ���ķ����ɵ�G�����꣮
��1����y=0ʱ��x2��2x��3=0����ã�x1=��1��x2=3����A����1��0����B��3��0�������������ߵĶԳ���Ϊֱ��x=1����x=0ʱ��y=x2��2x��3=��3����C��0����3����
��ֱ��BC�Ľ���ʽΪy=kx+b����B��3��0����C��0����3������ã�![]() ����ã�
����ã�![]() ������ֱ��BC�Ľ���ʽΪy=x��3��
������ֱ��BC�Ľ���ʽΪy=x��3��
��x=1ʱ��y=x��3=1��3=��2����D������Ϊ��1����2����
��2����ͼ1��
��B��3��0����C��0����3�������OBCΪ����ֱ�������Σ����OCB=��OBC=45�㣮
��D��1����2������CD![]() ������EDB=90��ʱ�����CDEΪ����ֱ�������Σ���CE
������EDB=90��ʱ�����CDEΪ����ֱ�������Σ���CE![]() CD
CD![]() 2����OE=3��2=1����ʱE��0����1�����൱m����1��m�٩�3ʱ����EDBΪ�۽ǣ���EDBΪ�۽������Σ�
2����OE=3��2=1����ʱE��0����1�����൱m����1��m�٩�3ʱ����EDBΪ�۽ǣ���EDBΪ�۽������Σ�
����EBD=90��ʱ�����OBEΪ����ֱ�������Σ���OE=OB=3����ʱE��0��3�����൱m��3ʱ����EDBΪ�۽ǣ���EDBΪ�۽������Σ�
��m��ȡֵ��ΧΪm��3��m����1��m�٩�3��
��3�����ڣ�
�ٵ���G�ڶԳ����Ҳ����������ʱ����ͼ2����DF��y����F��GH��DF��H����G��t��t2��2t��3������GH=t2��2t��3������2��=t2��2t��1��
������DE�Ƶ�D˳ʱ�뷽����ת90�㣬�������߽���ΪG�����EDG=90�㣬���EDF+��GDH=90�㣬����EDF+��DEF=90�㣬���DEF=��GDH����Rt��EDF��Rt��DGH����![]() ��������������ۣ�
��������������ۣ�
i����![]() 2����
2����![]() 2����t2��2t��1
2����t2��2t��1![]() ����ã�t1=1
����ã�t1=1![]() ����ȥ����t2=1
����ȥ����t2=1![]() ����ʱG������Ϊ��1
����ʱG������Ϊ��1![]() ����
����
ii����![]() ����
����![]() ����t2��2t��1=2����ã�t1=��1����ȥ����t2=3����ʱG������Ϊ��3��0����
����t2��2t��1=2����ã�t1=��1����ȥ����t2=3����ʱG������Ϊ��3��0����
�ڵ���G�ڶԳ���������������ʱ����ͬ���ķ����ɵ�G������Ϊ��1![]() ����1��0����
����1��0����
����������G��������1![]() ����3��0����1
����3��0����1![]() ����1��0����
����1��0����

 ���б�ˢ��ϵ�д�
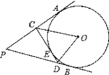
���б�ˢ��ϵ�д�����Ŀ��6��14������������Ѫ������ij�в�ȡ��Ը�����ķ�ʽ��֯����������Ѫ����ѪʱҪ����Ѫ�ߵ�Ѫ�ͽ��м�⣬���������A��������B��������AB��������O����4�����ͣ�����Ѫ����Ⱥ�У������ȡ�˲�����Ѫ�ߵ�Ѫ�ͽ������ͳ�ƣ����������ͳ�ƽ��������������������ͼ����
Ѫ�� | A | B | AB | O |
���� | �� �� | 10 | 5 | �� �� |
��1����������ȡ����Ѫ������Ϊ�� ���ˣ�m=�� ����
��2����ȫ�ϱ��е����ݣ�
��3������λ�и�����3000��������Ѫ��������ݳ�������ش�
����Ѫ����Ⱥ���γ�ȡһ�ˣ���Ѫ����A�͵ĸ����Ƕ��٣���������3000���д�Լ�ж�������A��Ѫ��

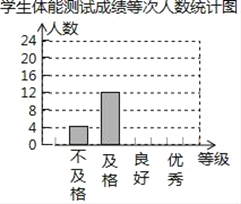
����Ŀ��ijУΪ�˽�ѧ������������Ӹ��꼶�����ȡ����ѧ���������ܲ��ԣ�ÿ��ѧ���IJ��Գɼ�������ӦΪ���㡢���á����������ĸ��ȼ���ͳ��Ա�ڽ��������ݻ��Ƴ�ͼ��ʱ���֣�����©ͳ��4�ˣ�����©ͳ��6�ˣ����Ǽ�ʱ�������Ӷ��γ���ͼͼ�����밴��ȷ���ݽ�����и��⣺
ѧ�����ܲ��Գɼ����ȴ�����ͳ�Ʊ�
���ܵȼ� | ����ǰ���� | ���������� |
���� | 8 | �� �� |
���� | 16 | �� �� |
���� | 12 | �� �� |
������ | 4 | �� �� |
�ϼ� | 40 | �� �� |
��1����дͳ�Ʊ���
��2�����ݵ��������ݣ���ȫ����ͳ��ͼ��
��3������У����ѧ��1500�ˣ�����������У���ܲ��Եȼ�Ϊ����������������