Question

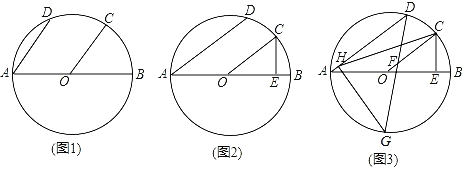
【题目】如图所示，的直径，、为圆周上两点，且，过点作，交的延长线于点．

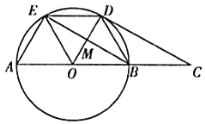
（1）求证：为切线；

（2）填空：①当四边形为菱形，则的度数为________；

②当时，四边形的面积为________．

Answer 1

【答案】（1）见详解；（2）①30°；②

【解析】

（1）根据题意可知，OD为半径，只需证明OD⊥DC即可；

（2）①若四边形AODE为菱形，可得出△AEO为等边三角形，结合∠AEB=90°，BE∥CD，得出∠C=∠ABE即可；

②根据条件，可证明△DOB为等边三角形，利用Rt△DOC和Rt△DON计算出△ODC的面积，以及菱形AODE的面积，相加即可得出四边形ACDE的面积．

（1）∵，

∴OD⊥BE，

∵BE∥CD，

∴OD⊥DC，

∵OD为半径，

∴CD为的切线；

（2）①∵四边形AODE为菱形，

∴AE=OE=AO，

∴△AEO为等边三角形，

∴∠EAO=60°，

∵∠AEB=90°，

∴∠ABE=30°，

∵BE∥CD，

∴∠C=∠ABE=30°，

故答案为：30°；

②作DN⊥AC交AC于N，

∵DB=DO=OB=AB，

∴△DOB为等边三角形，

∴∠DOB=60°，

在Rt△DOC和Rt△DON中，OD=2，∠DOC=60°，

∵DC=2，DN=，∠C=30°，

∴，

∵AODE为菱形，

∴，

∴四边形ACDE的面积=+=，

故答案为：．