题目内容
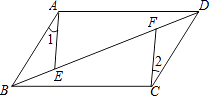
【题目】在ABCD中，AB=5，BC=10，BC边上的高AM=4，过BC边上的动点E（不与点B，C重合）作直线AB的垂线，EF与DC的延长线相交于点G．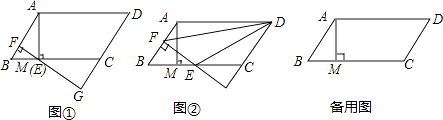
（1）如图①，当点E与点M重合时，求EF的长；
（2）如图②，当点E为BC的中点时，连结DE，DF，求△DEF的面积；
（3）当点E在BC上运动时，△BEF与△CEG的周长之间有何关系？请说明理由．
【答案】
（1）
解：如图①，
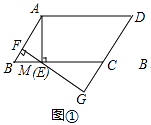
∵AB=5，AM=4，AM⊥BC，
∴BM= 
= 
=3，
∵S△ABM= 
AMBM= ABEF，
∴EF= 
= 
= 
．
（2）
解：如图②，
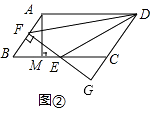
∵E为BC中点，BC=10，
∴BE=CE=5，
∴AB=BE=5，
∵EF⊥AB，AM⊥BC，
∴∠AMB=∠EFB=90°，
∵∠B=∠B，
∴△ABM≌△EBF，
∴EF=AM=4，BF=BM=3，
∵四边形ABCD为平行四边形，
∴AB∥DG，
∴FG⊥DG，∠B=∠ECG，
∵∠BFE=∠G=90°，
∴△BEF≌△CEG，
∴CG=BF=3，EF=EG=4，
∴DG=CD+CG=5+3=8，
∴S△DEF= EFDG= ×4×8=16；
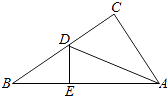
（3）
解：图③，
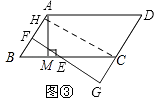
过点C作CH⊥AB，垂足为H，
∴HC⊥DG，
∴四边形HFGC为矩形，
∴HC=FG=8，CG=FH，
∴BH= 
= 
=6，
∵△BFE和△CEG的周长之和为：BE+EF+BF+EC+CG+EG，
=BC+FG+BH，
=10+8+6，
=24，
∴△BEE与△CEG的周长之和为定值24．
【解析】（1）先由勾股定理求BM的长，再利用面积法求EF；（2）要想求△DEF的面积，需要求底边EF和高DG的长，先证明△ABM≌△EBF，得EF=AM=4，再证明FG⊥DG，证明△BEF≌△CEG，得CG=3，求出DG=8，代入面积公式可以求△DEF的面积；（3）过点C作CH⊥AB，垂足为H，利用勾股定理求BH的长，写出△BEF与△CEG的周长之和，发现：EF+EG=FG=8，BF+CG=BH=6，从而求出面积和为24，是定值．
【考点精析】解答此题的关键在于理解三角形的面积的相关知识，掌握三角形的面积=1/2×底×高．
