Question

【题目】如图，有一块直角三角形纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD对折，使它落在斜边AB上，且与AE重合，求CD的长．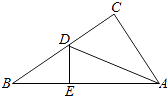

Answer 1

【答案】解：∵两直角边AC=6cm，BC=8cm，
在Rt△ABC中，由勾股定理可知AB=10，
现将直角边AC沿直线AD对折，使它落在斜边AB上，且与AE重合，则CD=DE，AE=AC=6，
∴BE=10﹣6=4，
设DE=CD=x，BD=8﹣x，
在Rt△BDE中，根据勾股定理得：BD2=DE2+BE2 ， 即（8﹣x）2=x2+42 ，
解得x=3．
即CD的长为3cm．
【解析】先由勾股定理求AB=10．再用勾股定理从△DEB中建立等量关系列出方程即可求CD的长．
【考点精析】通过灵活运用勾股定理的概念，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题．