题目内容
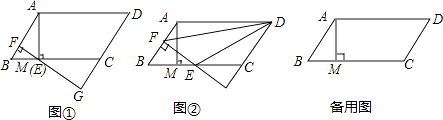
【题目】如图所示，已知∠OEB=130°，∠FOD=25°，OF平分∠EOD，试说明AB∥CD． 
【答案】证明：∵OF平分∠EOD， ∴∠FOD= 
∠EOD；
∵∠FOD=25°，
∴∠EOD=50°；
又∵∠OEB=130°，
∴∠OEB+∠EOD=180°，
∴AB∥CD（同旁内角互补，两直线平行）
【解析】根据角平分线的定义先求出∠EOD的度数，再利用同旁内角互补，两直线平行可证明AB∥CD．
【考点精析】认真审题，首先需要了解角的平分线(从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线)，还要掌握平行线的判定(同位角相等，两直线平行;内错角相等，两直线平行;同旁内角互补，两直线平行)的相关知识才是答题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某中学为了筹备校庆活动，准备印制一批校庆纪念册．该纪念册分A、B两种，每册都需要10张8K大小的纸，其中A纪念册有4张彩色页和6张黑白页组成；B纪念册有6张彩色页和4张黑白页组成．印制这批纪念册的总费用由制版费和印制费两部分组成，制版费与印数无关，价格为：彩色页300元∕张，黑白页50元∕张；印制费与总印数的关系见下表．
总印数a（单位：千册） | 1≤a＜5 | 5≤a＜10 |
彩色（单位：元∕张） | 2.2 | 2.0 |
黑白（单位：元∕张） | 0.7 | 0.5 |
（1）印制这批纪念册的制版费为多少元．
（2）若印制A、B两种纪念册各2千册，则共需多少费用？
（3）如果该校共印制了A、B两种纪念册6千册，一共花费了75500元，则该校印制了A、B两种纪念册各多少册？
