题目内容
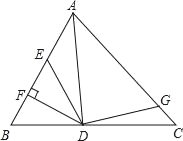
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为40和28,则△EDF的面积为( )
A. 12 B. 6 C. 7 D. 8
【答案】B
【解析】
过点D作DH⊥AC于H,根据角平分线上的点到角的两边距离相等可得DF=DH,再利用“HL”证明Rt△DEF和Rt△DGH全等,根据全等三角形的面积相等可得S△DEF=S△DGH,然后列式求解即可.
解:如图,过点D作DH⊥AC于H,
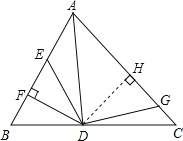
∵AD是△ABC的角平分线,DF⊥AB,
∴DF=DH,
在Rt△DEF和Rt△DGH中,
![]() ,
,
∴Rt△DEF≌Rt△DGH(HL),
∴S△DEF=S△DGH,
∵△ADG和△AED的面积分别为40和28,
∴△EDF的面积=![]() ×(40-28)=6.
×(40-28)=6.
故选:B.
【点晴】
本题考查了全等三角形的性质和判定及等面积法在解题中的应用,熟练掌握相关知识是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目