题目内容
如图,点A(m,m+1),B(m+1,2m-3)都在反比例函数 的图象上.
的图象上.
(1)求m,k的值;
(2)如果M为x轴上一点,N为y轴上一点, 以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.
(1)m=3,k=12;(2) 或
或
解析试题分析:(1)根据反比例函数图象上的点的坐标的特征可得 ,即可求得结果;
,即可求得结果;
(2)存在两种情况,①当M点在x轴的正半轴上,N点在y轴的正半轴上时,②当M点在x轴的负半轴上,N点在y轴的负半轴上时,根据平行四边形的性质求解即可.
(1)由题意可知,
解得m1=3,m2=-1(舍去)
∴A(3,4),B(4,3);
∴k=4×3=12;
(2)存在两种情况,如图:
①当M点在x轴的正半轴上,N点在y轴的正半轴上时,设M1点坐标为(x1,0),N1点坐标为(0,y1).
∵四边形AN1M1B为平行四边形,
∴线段N1M1可看作由线段AB向左平移3个单位,再向下平移3个单位得到的
由(1)知A点坐标为(3,4),B点坐标为(4,3),
∴N1点坐标为(0,1),M1点坐标为(1,0)
设直线M1N1的函数表达式为 ,把x=1,y=0代入,解得
,把x=1,y=0代入,解得 .
.
∴直线M1N1的函数表达式为 ;
;
②当M点在x轴的负半轴上,N点在y轴的负半轴上时,设M2点坐标为(x2,0),N2点坐标为(0,y2).
∵AB∥N1M1,AB∥M2N2,AB=N1M1,AB=M2N2,
∴N1M1∥M2N2,N1M1=M2N2.
∴线段M2N2与线段N1M1关于原点O成中心对称.
∴M2点坐标为(-1,0),N2点坐标为(0,-1).
设直线M2N2的函数表达式为 ,把x=-1,y=0代入,解得
,把x=-1,y=0代入,解得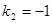 ,
,
∴直线M2N2的函数表达式为
所以,直线MN的函数表达式为 或
或 .
.
考点:反比例函数的综合题
点评:此类问题难度较大,在中考中比较常见,一般在压轴题中出现,需特别注意.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案如图,正比例函数y1=x的图象与反比例函数 (k≠0)的图象相交于A、B两点,点A的纵坐标为2.
(k≠0)的图象相交于A、B两点,点A的纵坐标为2.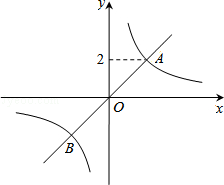
(1)求反比例函数的解析式;
(2)求出点B的坐标,并根据函数图象,写出当y1>y2时,自变量x的取值范围.
如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.∠EFB=65°,则∠AED′等于( ) 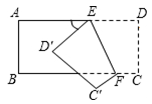
| A.70° | B.65° | C.50° | D.25° |
下列说法正确的是( ).
| A.买一张福利彩票一定中奖,是必然事件. |
| B.买一张福利彩票一定中奖,是不可能事件. |
C.抛掷一个正方体骰子,点数为奇数的概率是 . . |
| D.一组数据:1,7,3,5,3的众数是3. |
 ,经过点P(
,经过点P( ,
, ),点P关于
),点P关于 轴的对称点P′在反比例函数
轴的对称点P′在反比例函数 (
( )的图象上.
)的图象上.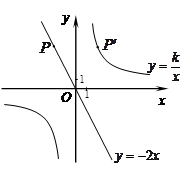
 的图象经过点C.
的图象经过点C.
 是等边
是等边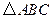 内一点,
内一点,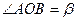 ,
,  .将
.将 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转 得
得 ,连接
,连接 .
.
 ,
, 时,试判断
时,试判断 的形状,并说明理由。
的形状,并说明理由。 为多少度,
为多少度, 的度数。
的度数。