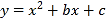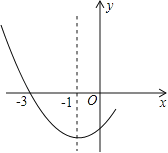题目内容
【题目】已知:已知二次函数的图象与![]() 轴交于
轴交于![]() 和
和![]() 两点.交
两点.交![]() 轴于点
轴于点![]() ,点
,点![]() ,
,![]() 是二次函数图象上的一对对称点,一次函数的图象过点
是二次函数图象上的一对对称点,一次函数的图象过点![]() ,
,![]()
(1)画出图象,并求二次函数的解析式.
(2)根据图象直接写出使一次函数值大于或等于二次函数值的![]() 的取值范围.
的取值范围.
(3)若直线与![]() 轴交点为
轴交点为![]() ,连接
,连接![]() ,
,![]() ,求三角形
,求三角形![]() 的面积.
的面积.
【答案】(1):![]() ;(2)
;(2)![]() 或
或![]() ;(3)4.
;(3)4.
【解析】
(1)直接将已知点代入函数解析式求出即可;(2)利用函数图像结合交点坐标得出使一次函数值大于或等于二次函数值的x的取值范围;(3)分别得出EO,AB的长,进而得出面积.
解:(1)设二次函数的解析式为![]() (
(![]() ,
,![]() 、
、![]() 、
、![]() 常数),
常数),
根据题意得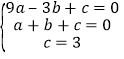 ,
,
解得: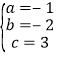 ,
,
所以二次函数的解析式为:![]() ;
;
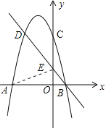
(2)如图,一次函数值大于二次函数值的![]() 的取值范围是:
的取值范围是:![]() 或
或![]() ;
;
(3)∵对称轴:![]() .
.
∴![]() ;
;
设直线![]() 代入
代入![]() ,
,![]() :
:
![]() ,
,
解得:![]() ,
,
故直线![]() 的解析式为:
的解析式为:![]() ,
,
把![]() 代入求得
代入求得
∴![]() ,
,
又∵![]()
∴![]() .
.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目