题目内容
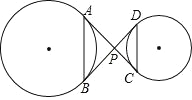
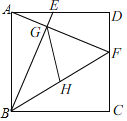
【题目】如图,在△ACD中,AD=9,CD=3![]() ,△ABC中,AB=AC.
,△ABC中,AB=AC.
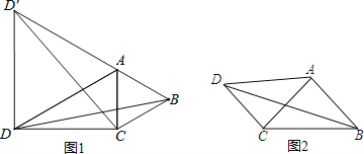
(1)如图1,若∠CAB=60°,∠ADC=30°,在△ACD外作等边△ADD′
①求证:BD=CD′;
②求BD的长.
(2)如图2,若∠CAB=90°,∠ADC=45°,求BD的长.
【答案】(1)①详见解析;②3![]() (2)6
(2)6![]()
【解析】
(1)①根据等边三角形的性质,可得![]() ,
,![]() ,
,![]() 由此可判定△BAD≌△CAD′,根据全等三角形对应边相等即可得出结论;②先证明∠CDD'=90°,在Rt CDD'中根据勾股定理即可求得BD;
由此可判定△BAD≌△CAD′,根据全等三角形对应边相等即可得出结论;②先证明∠CDD'=90°,在Rt CDD'中根据勾股定理即可求得BD;
(2)作AE⊥AD,使AE=AD,连接DE、CE,证明△BAD≌△CAE,即可得BD=CE,然后证明∠CDE=90°,根据勾股定理即可求得CE,由此可得BD.
(1)①证明:∵AB=AC,∠CAB=60°,
∴△ABC是等边三角形,
∴AC=AB=BC,
∵△ADD'是等边三角形,
∴AD=AD'=DD'=9,∠ADD'=∠DAD'=60°,
∴∠BAD=∠CAD',
在△BAD和△CAD′中, ,
,
∴△BAD≌△CAD′(SAS),
∴BD=CD';
②解:∵∠ADD'=60°,∠ADC=30°,
∴∠CDD'=90°,
∴CD'=![]() =
=![]() =3
=3![]() ,
,
∴BD=3![]() ;
;
(2)解:作AE⊥AD,使AE=AD,连接DE、CE,如图2所示:

则△ADE是等腰直角三角形,
∴∠ADE=45°,DE=![]() AD=9
AD=9![]() ,
,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即∠BAD=∠CAE,
在△BAD和△CAE中,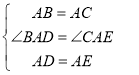 ,
,
∴△BAD≌△CAE(SAS),
∴BD=CE,
∵∠ADE=45°,∠ADC=45°,
∴∠CDE=90°,
∴CE=![]() =
=![]() =6
=6![]() ,
,
∴BD=6![]() .
.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目