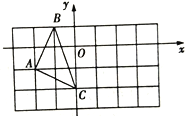
题目内容
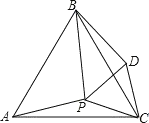
【题目】如图,在Rt△ABC中,AB=AC,P为斜边BC上一点(PB<CP),分别过点B,C作BE⊥AP于点E,CD⊥AP于点D.
(1)求证:AD=BE;
(2)若AE=2DE=2,求△ABC的面积.

【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据同角的余角相等可得∠BAE=∠ACD,根据"AAS"可证△ACD≌△BEA,可得AD=BE;(2)由题意可得AD=1,CD=2,根据勾股定理可求AC的长,根据三角形面积公式可求△ABC的面积.
证明:(1)∵∠BAC=90°,
∴∠BAE+∠CAD=90°,
∵CD⊥AD,
∴∠CAD+∠ACD=90°,
∴∠BAE=∠ACD,且AB=AC,∠AEB=∠ADC=90°,
∴△ACD≌△BEA(AAS),
∴AD=BE,AE=CD
(2)∵AE=2DE=2,AE=AD+DE,
∴AD=DE=1,AE=CD=2,
在Rt△ACD中,AC=![]() =
=![]() ,
,
∴AB=AC=![]() ,
,
∴S△ABC=![]() ×AB×AC=
×AB×AC=![]()

练习册系列答案
相关题目
【题目】为了参加“荆州市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77,92,85;八(2)班79,85,92,85,89.通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 | 方差 |
八(1) | 85 | b | c | 22.8 |
八(2) | a | 85 | 85 | 19.2 |
(1)直接写出表中a,b,c的值;
(2)根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.