题目内容
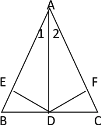
【题目】已知Rt△ABC的斜边AB=6 cm,直角边AC=3 cm.
(1)以C为圆心，2 cm长为半径的圆和AB的位置关系是_________；
(2)以C为圆心，4 cm长为半径的圆和AB的位置关系是_________；
(3)如果以C为圆心的圆和AB相切，则半径长为_________。
【答案】 相离 相交 
cm
【解析】
设⊙O的半径为r，圆心O到直线的距离为d，那么：
直线与⊙O相交d<r；
直线与⊙O相切d=r；
直线与⊙O相离d>r．
先求出另一条直角边和斜边上的高，可得答案.
由已知可得，BC=
,
所以，斜边上的高CD=
,
（1）因为2<,所以，以C为圆心，2 cm长为半径的圆和AB的位置关系是相离；
（2）因为4>,所以，以C为圆心，4 cm长为半径的圆和AB的位置关系是相交；
(3)如果以C为圆心的圆和AB相切，则半径长为cm.
故答案为：(1). 相离 (2). 相交 (3). cm
练习册系列答案
阅读快车系列答案
相关题目
【题目】探究函数y=x+
（x＞0）与y=x+
（x＞0，a＞0）的相关性质．
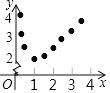
（1）小聪同学对函数y=x+（x＞0）进行了如下列表、描点，请你帮他完成连线的步骤；观察图象可得它的最小值为 ，它的另一条性质为 ；
x | … |
|
|
| 1 |
| 2 |
| 3 | … |
y | … |
|
|
| 2 |
|
|
|
| … |
（2）请用配方法求函数y=x+（x＞0）的最小值；
（3）猜想函数y=x+（x＞0，a＞0）的最小值为 ．
