Question

【题目】直角三角形中，，直线过点．

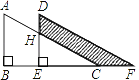
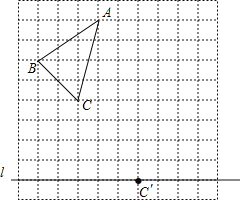
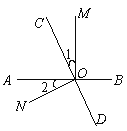
（1）当时，如图①，分别过点、作于点，于点．求证：．

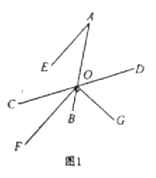
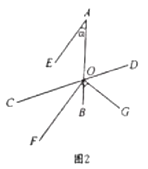
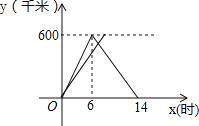
（2）当，时，如图②，点与点关于直线对称，连接、，动点从点出发，以每秒1个单位长度的速度沿边向终点运动，同时动点从点出发，以每秒3个单位的速度沿向终点运动，点、到达相应的终点时停止运动，过点作于点，过点作于点，设运动时间为秒．

①用含的代数式表示．

②直接写出当与全等时的值．

Answer 1

【答案】（1）证明见解析；（2）①CN=6-3t；（2）3.5秒或5秒或6.5秒

【解析】

（1）根据垂直的定义得到∠DAC=∠ECB，利用AAS定理证明△ACD≌△CBE；

（2）①由题意得，AM=t，FN=3t，则CM=8-t，由折叠的性质可知，CF=CB=6，即可得出结果；

②分点F沿F→C路径运动，点F沿C→B路径运动，点F沿B→C路径运动，点F沿C→F路径运动四种情况，根据全等三角形的判定定理列式计算．

（1）证明：△ACD与△CBE全等．

理由如下：∵AD⊥直线l，

∴∠DAC+∠ACD=90°，

∵∠ACB=90°，

∴∠BCE+∠ACD=90°，

∴∠DAC=∠ECB，

在△ACD和△CBE中，

，

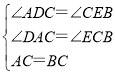∴△ACD≌△CBE（AAS）；

（2）解：①由题意得，AM=t，FN=3t，

则CM=8-t，

由折叠的性质可知，CF=CB=6，

∴CN=6-3t；

②由折叠的性质可知，∠BCE=∠FCE，

∵∠MCD+∠CMD=90°，∠MCD+∠BCE=90°，

∴∠NCE=∠CMD，

∴当CM=CN时，△MDC与△CEN全等，

当点F沿F→C路径运动时，8-t=6-3t，

解得，t=-1（不合题意），

当点F沿C→B路径运动时，8-t═3t-6，

解得，t=3.5，

当点F沿B→C路径运动时，由题意得，8-t=18-3t，

解得，t=5，

当点F沿C→F路径运动时，由题意得，8-t=3t-18，

解得，t=6.5，

综上所述，当t=3.5秒或5秒或6.5秒时，△MDC与△CEN全等．