题目内容
【题目】A、B两地相距600千米,甲、乙两车同时从A地出发驶向B地,甲车到达B地后立即返回,它们各自离A地的距离y(千米)与行驶时间x(时)之间的函数关系图象如图所示.
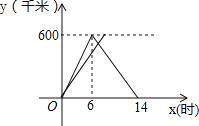
(1)求甲车行驶过程中y与x之间的函数关系式;
(2)当它们行驶了7小时时,两车相遇,求乙车的速度.
【答案】(1)y=![]() ;(2)乙车的速度为75千米/时.
;(2)乙车的速度为75千米/时.
【解析】
(1)根据函数图象可以得到甲车行驶过程中y与x之间的函数关系式;
(2)根据(1)求得函数解析式,可以得到当x=7时的y值,然后用求得的y值除以7即可求得乙车的速度.
解:(1)当0≤x≤6时,设甲车行驶过程中y与x之间的函数关系式为y=mx,
把(6,600)代入y=mx,
6m=600,
解得m=100,
∴y=100x;
当6<x≤14时,设甲车行驶过程中y与x之间的函数关系式为y=kx+b,
把(6,600)、(14,0)代入y=kx+b,
得![]() ,
,
解得,![]() ,
,
∴y=﹣75x+1050;
即甲车行驶过程中y与x之间的函数关系式为:y=![]() ;
;
(2)当x=7时,y=﹣75x+1050
解得,y=﹣75×7+1050=525,
525÷7=75(千米/时),
即乙车的速度为75千米/时.

练习册系列答案
相关题目