题目内容
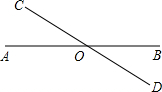 如图,已知直线AB和CD相交于点O(∠AOC为锐角)
如图,已知直线AB和CD相交于点O(∠AOC为锐角)(1)写出∠AOC和∠BOD的大小关系
∠AOC=∠BOD
∠AOC=∠BOD
;判断的依据是对顶角相等
对顶角相等
.(2)过点O作射线OE、OF,若∠COE=90°,OF平分∠AOE,画出图形并求∠AOF+∠COF的度数,说明你的理由.
(3)在(2)的条件下,若∠AOD=120°,请计算∠COF的度数.
分析:(1)根据对顶角相等的性质解答;
(2)根据角平分线的定义可得∠AOF=∠EOF,然后求出∠AOF+∠COF=∠EOF+∠COF=∠COE,即可得解;
(3)根据邻补角的定义求出∠AOC,再分①OE在∠BOC内部时,先求出∠AOE,然后根据角平分线的定义求出∠AOF,最后根据∠COF=∠AOF-∠AOC代入数据进行计算即可得解;②OE在∠AOD内部时,先求出∠AOE,然后根据角平分线的定义求出∠AOF,最后根据∠COF=∠AOF+∠AOC代入数据进行计算即可得解.
(2)根据角平分线的定义可得∠AOF=∠EOF,然后求出∠AOF+∠COF=∠EOF+∠COF=∠COE,即可得解;
(3)根据邻补角的定义求出∠AOC,再分①OE在∠BOC内部时,先求出∠AOE,然后根据角平分线的定义求出∠AOF,最后根据∠COF=∠AOF-∠AOC代入数据进行计算即可得解;②OE在∠AOD内部时,先求出∠AOE,然后根据角平分线的定义求出∠AOF,最后根据∠COF=∠AOF+∠AOC代入数据进行计算即可得解.
解答:解:(1)∠AOC=∠BOD,判断的依据是对顶角相等;
(2)∵OF平分∠AOE,
∴∠AOF=∠EOF,
∴∠AOF+∠COF=∠EOF+∠COF=∠COE,
∵∠COE=90°,
∴∠AOF+∠COF=90°;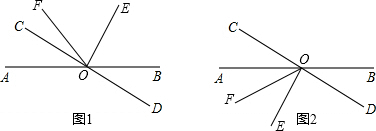
(3)∵∠AOD=120°,
∴∠AOC=180°-∠AOD=180°-120°=60°,
①OE在∠BOC内部时,如图1,∠AOE=∠AOC+∠COE=60°+90°=150°,
∵OF平分∠AOE,
∴∠AOF=
∠AOE=
×150°=75°,
∴∠COF=∠AOF-∠AOC=75°-60°=15°;
②OE在∠AOD内部时,如图2,∠AOE=∠COE-∠AOC=90°-60°=30°,
∵OF平分∠AOE,
∴∠AOF=
∠AOE=
×30°=15°,
∴∠COF=∠AOF+∠AOC=15°+60°=75°;
综上所述,∠COF的度数是15°或75°.
(2)∵OF平分∠AOE,
∴∠AOF=∠EOF,
∴∠AOF+∠COF=∠EOF+∠COF=∠COE,
∵∠COE=90°,
∴∠AOF+∠COF=90°;

(3)∵∠AOD=120°,
∴∠AOC=180°-∠AOD=180°-120°=60°,
①OE在∠BOC内部时,如图1,∠AOE=∠AOC+∠COE=60°+90°=150°,
∵OF平分∠AOE,
∴∠AOF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠COF=∠AOF-∠AOC=75°-60°=15°;
②OE在∠AOD内部时,如图2,∠AOE=∠COE-∠AOC=90°-60°=30°,
∵OF平分∠AOE,
∴∠AOF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠COF=∠AOF+∠AOC=15°+60°=75°;
综上所述,∠COF的度数是15°或75°.
点评:本题考查了对顶角相等,邻补角互补的定义,角平分线的定义,角的计算,是基础题,熟记性质是解题的关键,难点在于要分情况讨论,作出图形更形象直观.

练习册系列答案
相关题目
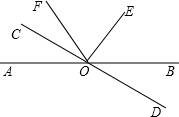 如图,已知直线AB和CD相交于O点,∠DOE是直角,OF平分∠AOE,∠BOD=22°,求∠COF的度数.
如图,已知直线AB和CD相交于O点,∠DOE是直角,OF平分∠AOE,∠BOD=22°,求∠COF的度数. (2013•奉贤区二模)如图,已知直线AB和CD相交于点O,OE⊥AB,∠AOD=128°,则∠COE的度数是
(2013•奉贤区二模)如图,已知直线AB和CD相交于点O,OE⊥AB,∠AOD=128°,则∠COE的度数是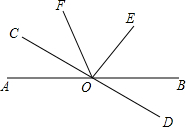 (1)已知一个角的余角是这个角的补角的
(1)已知一个角的余角是这个角的补角的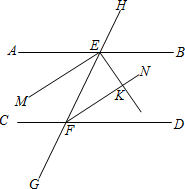 如图,已知直线AB和直线CD被直线GH所截,交点分别为E、F点,且AB∥CD.
如图,已知直线AB和直线CD被直线GH所截,交点分别为E、F点,且AB∥CD.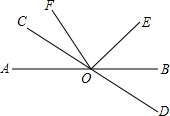 如图,已知直线AB和CD相交于O点,∠COE是直角,OF平分∠AOE,∠COF=34°,则∠BOD的大小为
如图,已知直线AB和CD相交于O点,∠COE是直角,OF平分∠AOE,∠COF=34°,则∠BOD的大小为