��Ŀ����
����Ŀ���Ķ����в��ϣ�������⣺
���壺�߶�AD�ѵ���������ABC�ֳɡ�ABD���ACD����ͼ1���������ABD���ACD��Ϊ���������Σ���ô�߶�AD������ABC�������ָ���.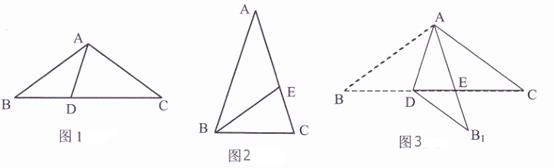
��1����ͼ1����֪��ABC�У�AB=AC����BAC=108�㣬ADΪ��ABC�������ָ��ߣ���BD<CD�����B= �� ��ADC=.
��2����ͼ2����֪��ABC�У�AB=AC����A=36�㣬BEΪ��ABC�Ľ�ƽ���ߣ���֤��BEΪ��ABC�����ָ���.
��3����ͼ3����֪��ABC��һ����������ֽƬ��AB=AC��AD������һ�������ָ��ߣ�����ABD��ֱ��AD�۵���B���ڵ�B1����AB1��CD�ڵ�E����֤��DB1=EC.
���𰸡�
��1��36o��72o
��2��
֤������AB=AC
���ABC=��C= ![]()
��BEΪ��ABC�Ľ�ƽ����
�� ![]()
���ABE=��A
��AE=BE�ߡ�BEC=180�C��C�C��CBE=72
���BEC=��C
��BE=BC
���ABE����BEC������������
��BEΪ��ABC�������ָ��ߣ�
��3��
֤������AD�ǡ�ABC��һ�������ָ���
��AD=BD��AC=CD
���B=��BAD����CAD=��CDA
�ߡ�B+��BAD+��ADB=180����ADB+��CDA=180
���CDA=��B+��BAD=2��BAD
���CAD=2��BAD
�ߡ�BAD=��B1AD
���CAD=2��B1AD
�ߡ�CAD=��B1AD+��CAE
���B1AD=��CAE
��AB=AC
���B=��C
�ߡ�B=��B1
���B1=��C
��AB=AB1
��AB1= AC
���AB1D�ա�ACE
��DB1=CE
���������⣺��1����AB=AC����BAC=108�㣬���B= ![]() =36�㣬��ADΪ��ABC�������ָ��ߣ�BD<CD����AC=AD��BD=AD�����ADC=
=36�㣬��ADΪ��ABC�������ָ��ߣ�BD<CD����AC=AD��BD=AD�����ADC= ![]() 72��.
72��.
���Դ���72��.

 ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
ȫ�ŵ�����Ԫ�ƻ�ϵ�д�����Ŀ��һ����ѧ���ᄊ�˶����ϣ�21���μ�����������Ŀ���˶�Ա�ɼ��y�����£�
�ɼ���m�� | 1.50 | 1.55 | 1.60 | 1.65 | 1.70 |
���� | �� | 8 | 6 | �� | 1 |
�������������ݱ���ˮ�ܻ�ģ�����ˣ�����������������ȷ����ͳ�����ǣ� ��
A.ƽ����B.��λ��C.����D.����
����Ŀ���±���ijУ�������20�����꼶����������ͳ�Ʊ���
���ߣ�cm�� | 150 | 155 | 160 | 163 | 165 | 168 |
�������ˣ� | 1 | 3 | 4 | 4 | 5 | 3 |
�������ݵ�������__cm����λ����__cm��