题目内容
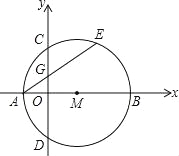
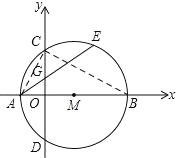
【题目】如图,在平面直角坐标系xOy中,点m在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C,D两点,且C为弧AE的中点,AE交y轴于G点,若点A的坐标为(﹣2,0),AE=8,
(1)求证:AE=CD;
(2)求点C坐标和⊙M直径AB的长;
(3)求OG的长.
【答案】(1)证明见解析(2)(0,4),10(3)![]()
【解析】
试题分析:(1)要证明AE=CD,即证明![]() ,由点C是
,由点C是![]() 的中点和AB⊥CD可知,
的中点和AB⊥CD可知,![]() ,从而可得
,从而可得![]() ;
;
(2)由垂径定理可知:OC=![]() CD=
CD=![]() AE=4,所以点C的坐标为(0,4),连接AC和BC后,证明△CAO∽△BAC,可得CA2=AOAB,从而可求出AB的长度;
AE=4,所以点C的坐标为(0,4),连接AC和BC后,证明△CAO∽△BAC,可得CA2=AOAB,从而可求出AB的长度;
(3)由![]() 可知,AG=CG,设AG=x,则OG=4﹣x,利用勾股定理可列出方程即可求出x的值.
可知,AG=CG,设AG=x,则OG=4﹣x,利用勾股定理可列出方程即可求出x的值.
试题解析:(1)∵点C是![]() 的中点,
的中点,
∴![]() ,
,
∵AB⊥CD,
∴由垂径定理可知:![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴AE=CD;
(2)连接AC、BC,
由(1)可知:CD=AE=8,
∴由垂径定理可知:OC=![]() CD=4,
CD=4,
∴C的坐标为(0,4),
由勾股定理可求得:CA2=22+42=20,
∵AB是⊙M的直径,
∴∠ACB=90°,
∵∠CAB=∠CAB,
∴△CAO∽△BAC,
∴![]() ,
,
∴CA2=AOAB,
∴AB=![]() =10;
=10;
(3)由(1)可知:![]() ,
,
∴∠ACD=∠CAE,
∴AG=CG,
设AG=x,
∴CG=x,OG=OC﹣CG=4﹣x,
∴由勾股定理可求得:AO2+OG2=AG2,
∴22+(4﹣x)2=x2,
∴x=![]() ,
,
∴OG=4﹣x=![]()

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目