Question

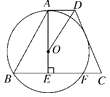
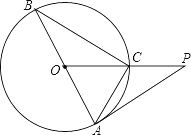
【题目】如图，△ABC内接于⊙O，AB是⊙O的直径，∠BAC=2∠B，⊙O的切线AP与OC的延长线相交于点P，若PA= 6cm，求AC的长．

四、综合题（10分）

Answer 1

【答案】6cm.

【解析】试题分析: 由AB是⊙O的直径和∠BAC=2∠B,根据圆周角定理和三角形内角和定理可得∠BAC=600,等边三角形的判定知△OAC是等边三角形,由PA是⊙O的切线得

Rt△OAP中,PA=6cm,∠AOP=60°,从而应用锐角三角函数即可求得OA=AC的长.

试题解析:∵AB是⊙O直径, ∴∠ACB=90°,

∵∠BAC=2∠B,

∴∠B=30°,∠BAC=60°,

∵OA=OC,

∴△AOC是等边三角形,

∴∠AOC=60°,AC=OA,

∵PA是⊙O切线,

∴∠OAP=90°,

在Rt△OAP中,PA=6cm,∠AOP=60°,

∴OA= =6cm,

∴AC=OA=6cm.