题目内容
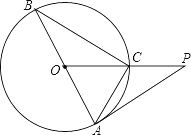
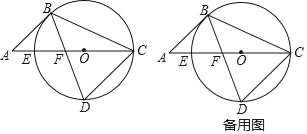
【题目】如图,已知CE是圆O的直径,点B在圆O上由点E顺时针向点C运动(点B不与点E、C重合),弦BD交CE于点F,且BD=BC,过点B作弦CD的平行线与CE的延长线交于点A.
(1)若圆O的半径为2,且点D为弧EC的中点时,求圆心O到弦CD的距离;
(2)当DFDB=CD2时,求∠CBD的大小;
(3)若AB=2AE,且CD=12,求△BCD的面积.
【答案】(1)![]() ;(2)45°;(3)72.
;(2)45°;(3)72.
【解析】试题分析:(1)过O作OH⊥CD于H,根据垂径定理求出点O到H的距离即可;
(2)根据相似三角形的判定与性质,先证明△CDF∽△BDC,再根据相似三角形的性质可求解;
(3)连接BE,BO,DO,并延长BO至H点,利用相似三角形的性质判定,求得BH的长,然后根据三角形的面积求解即可.
试题解析:(1)如图,过O作OH⊥CD于H,
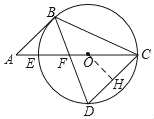
∵点D为弧EC的中点,
∴弧ED=弧CD,
∴∠OCH=45°,
∴OH=CH,
∵圆O的半径为2,即OC=2,
∴OH=![]() ;
;
(2)∵当DFDB=CD2时,![]() ,
,
又∵∠CDF=∠BDC,
∴△CDF∽△BDC,
∴∠DCF=∠DBC,
∵∠DCF=45°,
∴∠DBC=45°;
(3)如图,连接BE,BO,DO,并延长BO至H点,
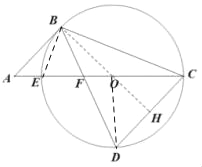
∵BD=BC,OD=OC,
∴BH垂直平分CD,
又∵AB∥CD,
∴∠ABO=90°=∠EBC,
∴∠ABE=∠OBC=∠OCB,
又∵∠A=∠A,
∴△ABE∽△ACB,
∴![]() ,即AB2=AE×AC,
,即AB2=AE×AC,
∴AC=![]() ,
,
设AE=x,则AB=2x,
∴AC=4x,EC=3x,
∴OE=OB=OC=![]() ,
,
∵CD=12,
∴CH=6,
∵AB∥CH,
∴△AOB∽△COH,
∴![]() ,即
,即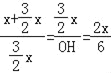 ,
,
解得x=5,OH=4.5,OB=7.5,
∴BH=BO+OH=12,
∴△BCD的面积=![]() ×12×12=72.
×12×12=72.

练习册系列答案
相关题目