题目内容
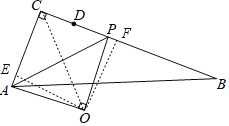
【题目】如图,Rt△ABC中,∠C=90°,AC=2,BC=5,点D是BC边上一点且CD=1,点P是线段DB上一动点,连接AP,以AP为斜边在AP的下方作等腰Rt△AOP.当P从点D出发运动至点B停止时,点O的运动路径长为_____.

【答案】2![]()
【解析】过O点作OE⊥CA于E,OF⊥BC于F,连接CO,如图,易得四边形OECF为矩形,由△AOP为等腰直角三角形得到OA=OP,∠AOP=90°,则可证明△OAE≌△OPF,所以AE=PF,OE=OF,根据角平分线的性质定理的逆定理得到CO平分∠ACP,从而可判断当P从点D出发运动至点B停止时,点O的运动路径为一条线段,接着证明CE=![]() (AC+CP),然后分别计算P点在D点和B点时OC的长,从而计算它们的差即可得到P从点D出发运动至点B停止时,点O的运动路径长.
(AC+CP),然后分别计算P点在D点和B点时OC的长,从而计算它们的差即可得到P从点D出发运动至点B停止时,点O的运动路径长.
过O点作OE⊥CA于E,OF⊥BC于F,连接CO,如图,
∵△AOP为等腰直角三角形,
∴OA=OP,∠AOP=90°,
易得四边形OECF为矩形,
∴∠EOF=90°,CE=CF,
∴∠AOE=∠POF,
∴△OAE≌△OPF,
∴AE=PF,OE=OF,
∴CO平分∠ACP,
∴当P从点D出发运动至点B停止时,点O的运动路径为一条线段,
∵AE=PF,
即AC-CE=CF-CP,
而CE=CF,
∴CE=![]() (AC+CP),
(AC+CP),
∴OC=![]() CE=
CE=![]() (AC+CP),
(AC+CP),
当AC=2,CP=CD=1时,OC=![]() ×(2+1)=
×(2+1)=![]() ,
,
当AC=2,CP=CB=5时,OC=![]() ×(2+5)=
×(2+5)=![]() ,
,
∴当P从点D出发运动至点B停止时,点O的运动路径长=![]() -
-![]() =2
=2![]() .
.
故答案为2![]() .
.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案【题目】小华根据学习函数的经验,对函数![]() 的图象与性质进行了研究,下面是小华的研究过程,请补充完成.
的图象与性质进行了研究,下面是小华的研究过程,请补充完成.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
| 4 | 5 |
|
|
| m | 2 | 1 | 0 | n | 2 | 3 |
|
其中,m= ,n= ;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出该函数的图象;

(3)观察图象,写出该函数的两条性质;
(4)进一步研究函数图象发现:
①方程![]() 有 个实数根;
有 个实数根;
②不等式![]() 的解集为 .
的解集为 .