题目内容
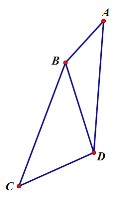
【题目】如图所示，AB=AC，AD=AE，∠BAC=∠DAE，∠1=25°，∠2=30°
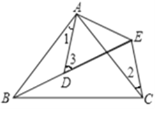
（1）求证△ABD≌△ACE
（2）求∠3度数.
【答案】（1）见解析；（2）51°.
【解析】
根据∠BAC=∠DAE通过角的计算即可得出∠1=∠CAE，结合AB=AC、AD=AE即可证出△BAD≌△CAE（SAS），进而即可得出∠ABD=∠2=30°．再根据外角的性质即可得出∠3的度数．
（1）∵∠BAC=∠DAE，∠BAC=∠1+∠DAC，∠DAE=∠DAC+∠CAE，
∴∠1=∠CAE.
在△ABD和△ACE中,
，
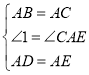∴△ABD≌△ACE (SAS)，
（2） ∴∠ABD=∠2=30°.
∵∠3=∠1+∠ABD=21°+30°=51°，
故答案为：51°.
练习册系列答案
相关题目
