题目内容
已知：在△ABC中，∠A=60°，∠B=45°，AC=2，则AB的长为______．
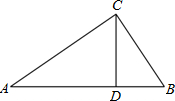
如右图所示，过C作CD⊥AB于D，
∵CD⊥AB，
∴∠ADC=∠BDC=90°，
在Rt△ADC中，∠A=60°，∠ADC=90°，
∴∠ACD=30°，
∴AD=
AC=1，
∴CD=
=
=
，
在Rt△BCD中，∠B=45°，∠BDC=90°，
∴∠BCD=45°，
∴BD=CD=
，
∴AB=AD+BD=1+
．
故答案为：1+
．
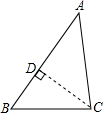
∵CD⊥AB，
∴∠ADC=∠BDC=90°，
在Rt△ADC中，∠A=60°，∠ADC=90°，
∴∠ACD=30°，
∴AD=
| 1 |
| 2 |
∴CD=
| AC2-AD2 |
| 22-12 |
| 3 |
在Rt△BCD中，∠B=45°，∠BDC=90°，
∴∠BCD=45°，
∴BD=CD=
| 3 |
∴AB=AD+BD=1+
| 3 |
故答案为：1+
| 3 |
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
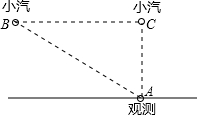车速检测仪间距离为50m，这辆小汽车超速了吗？（参考数据转换：1m/s=3.6km/h）
