题目内容
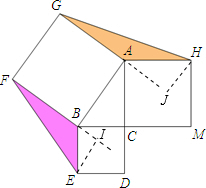
如图,以Rt△ABC的三边为边向外分别作正方形ACMH,正方形BCDE,正方形ABFG,连结EF,GH,已知∠ACB=90°,BC=t,AC=2-t(0<t<1).若图中阴影部分的面积和为0.84,则t=______.


过E做EI垂直FB的延长线与I,
∵∠ABC+∠FBE=180°,∠EBI+∠FBE=180°
∴∠ABC=∠EBI,
又∵∠ACB=∠EIB=90°
∴
=
,
∴AB•EI=BE•AC,
∴S△EBF=
EI•BF=
BE•AC=
(2t-t2),
过H做HJ垂直GA的延长线与J,
同理可证△HAJ∽△BAC,
∴
=
,
∴HJ•AC=AH•BC,
∴S△HAG=
HJ•AC=
AH•BC=
(2t-t2),
∵S△EBF+S△HAG=0.84,
∴
(2t-t2)+
(2t-t2)=0.84,
解得t=0.6,
故答案为0.6.
∵∠ABC+∠FBE=180°,∠EBI+∠FBE=180°
∴∠ABC=∠EBI,
又∵∠ACB=∠EIB=90°
∴
| AB |
| BC |
| AC |
| EI |

∴AB•EI=BE•AC,
∴S△EBF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
过H做HJ垂直GA的延长线与J,
同理可证△HAJ∽△BAC,
∴
| AH |
| AC |
| HJ |
| BC |
∴HJ•AC=AH•BC,
∴S△HAG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵S△EBF+S△HAG=0.84,
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得t=0.6,
故答案为0.6.

练习册系列答案
相关题目






