题目内容
要在一个半径为2
m的圆形钢板上裁出一块面积最大的正方形,该正方形的边长是______m.
| 2 |
设该正方形的边长为x,则:
要想裁出一块面积最大的正方形,需要正方形边长最长,所以正方形的四个顶点在圆周上,
如下图所示:
连接OA,过O作OE⊥AD交AD与E,则:
OA=2
,AE=OE=
,
在Rt△AEO中,由勾股定理得:
OE=
=
=
解得x=4
∴该正方形的边长为4m
故此题应该填4.
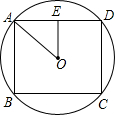
要想裁出一块面积最大的正方形,需要正方形边长最长,所以正方形的四个顶点在圆周上,
如下图所示:
连接OA,过O作OE⊥AD交AD与E,则:
OA=2
| 2 |
| x |
| 2 |
在Rt△AEO中,由勾股定理得:
OE=
| AO2-AE2 |
(2
|
| x |
| 2 |
解得x=4
∴该正方形的边长为4m
故此题应该填4.


练习册系列答案
相关题目





