题目内容
如图,二次函数y=ax2+bx+c的图象交x轴于A(-2,0),B(1,0),交y轴于C(0,-2),过B、C画直线.
(1)求二次函数的解析式;
(2)点P在x轴负半轴上,且PB=PC,求OP的长;
(3)点M在二次函数图象上,过M向直线BC作垂线,垂足为H.若M在y轴左侧,且△CHM∽△BOC,求点M的坐标.
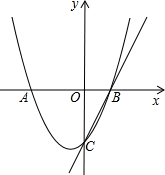
(1)求二次函数的解析式;
(2)点P在x轴负半轴上,且PB=PC,求OP的长;
(3)点M在二次函数图象上,过M向直线BC作垂线,垂足为H.若M在y轴左侧,且△CHM∽△BOC,求点M的坐标.

(1)∵二次函数y=ax2+bx+c的图象交x轴于A(-2,0),B(1,0),
∴设该二次函数的解析式为:y=a(x+2)(x-1),
将x=0,y=-2代入,得-2=a(0+2)(0-1),
解得a=1,
∴抛物线的解析式为y=(x+2)(x-1),即y=x2+x-2;
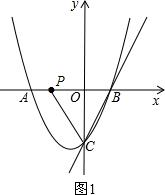
(2)如图1.由(1)知,抛物线的解析式为y=x2-x-2,则C(0,-2).
设OP=x,则PB=PC=x+1,
在Rt△POC中,由勾股定理,得x2+22=(x+1)2,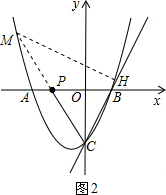
解得,x=
,即OP=
;
(3)∵△CHM∽△BOC,
∴∠MCH=∠CBO.
(i)如图2,当点H在点C上方时.
由(2)知,PB=PC,
∴∠PCB=∠CBP,即∠PCB=∠CBO.
又∵∠MCH=∠CBO,即∠MCB=∠CBO,
∴∠PCB=∠MCB,
∴点M是线段CP的延长线与抛物线的交点.
设直线CM的解析式为y=kx-2(k≠0),
把P(-
,0)代入,得-
k-2=0,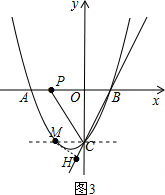
解得,k=-
,则直线CM的解析式是y=-
x-2,
∴
,
解得,
(舍去),或
,
∴M(-
,
);
(ii)如图3,点H在点C下方时.
∵∠MCH=∠CBO,
∴CM∥x轴,
∴yM=-2,
∴x2+x-2=-2,
解得x1=0(舍去),x2=-1
∴M(-1,-2).
综上所述,点M的坐标是M(-
,
)或M(-1,-2).
∴设该二次函数的解析式为:y=a(x+2)(x-1),
将x=0,y=-2代入,得-2=a(0+2)(0-1),
解得a=1,
∴抛物线的解析式为y=(x+2)(x-1),即y=x2+x-2;
(2)如图1.由(1)知,抛物线的解析式为y=x2-x-2,则C(0,-2).
设OP=x,则PB=PC=x+1,
在Rt△POC中,由勾股定理,得x2+22=(x+1)2,

解得,x=
| 3 |
| 2 |
| 3 |
| 2 |
(3)∵△CHM∽△BOC,
∴∠MCH=∠CBO.
(i)如图2,当点H在点C上方时.
由(2)知,PB=PC,
∴∠PCB=∠CBP,即∠PCB=∠CBO.
又∵∠MCH=∠CBO,即∠MCB=∠CBO,
∴∠PCB=∠MCB,
∴点M是线段CP的延长线与抛物线的交点.
设直线CM的解析式为y=kx-2(k≠0),
把P(-
| 3 |
| 2 |
| 3 |
| 2 |

解得,k=-
| 4 |
| 3 |
| 4 |
| 3 |
∴
|
解得,
|
|
∴M(-
| 7 |
| 3 |
| 10 |
| 9 |
(ii)如图3,点H在点C下方时.
∵∠MCH=∠CBO,
∴CM∥x轴,
∴yM=-2,
∴x2+x-2=-2,
解得x1=0(舍去),x2=-1
∴M(-1,-2).
综上所述,点M的坐标是M(-
| 7 |
| 3 |
| 10 |
| 9 |


练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 -2,0),B(-1,-3).
-2,0),B(-1,-3).