Question

【题目】如图，AD⊥BC于点D，∠B=∠DAC，点E在BC上，△EAC是以EC为底的等腰三角形，AB=4，AE=3．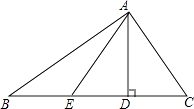

（1）判断△ABC的形状；
（2）求△ABC的面积．

Answer 1

【答案】
（1）解：∵AD⊥BC，

∴∠ADB=90°，

∴∠B+∠BAD=90°，

∵∠B=∠DAC，

∴∠DAC+∠BAD=90°，即∠BAC=90°，

∴△ABC是直角三角形

（2）解：∵△EAC是等腰三角形，

∴AC=AE=3，

∴△ABC的面积= ×AB×AC= ×4×3=6

【解析】（1）根据AD⊥BC，∠B=∠DAC，求得∠BAC的度数即可；（2）先根据△EAC是等腰三角形，得出AC=AE=3，再计算△ABC的面积．
【考点精析】本题主要考查了等腰三角形的性质的相关知识点，需要掌握等腰三角形的两个底角相等（简称：等边对等角）才能正确解答此题．