题目内容
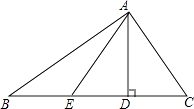
【题目】已知,如图,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE,CD相交于点F,求证:∠CEF=∠CFE. 
【答案】证明:∵∠ACB=90°,CD是高,
∴∠ACD+∠CAB=90°,∠B+∠CAB=90°,
∴∠ACD=∠B;
∵AE是角平分线,
∴∠CAE=∠BAE;
∵∠CFE=∠CAE+∠ACD,∠CEF=∠BAE+∠B,
∴∠CFE=∠CEF
【解析】先根据在△ABC中,∠ACB=90°,CD是高可得出∠ACD+∠CAB=90°,∠B+∠CAB=90°,故∠ACD=∠B,再根据AE是角平分线可知∠CAE=∠BAE,进而可得出结论.
【考点精析】掌握三角形的内角和外角是解答本题的根本,需要知道三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

练习册系列答案
相关题目
【题目】学校团委组织80名新团员为学校建“实践活动园地”搬砖.女同学每人般3块,男同学每人搬4块,共搬了290块.
(1)设新团员中有x名男同学,请你把表格补充完整:
男同学 | 女同学 | 总数 | |
参加人数(名) | x | 80 | |
每人搬砖数(块) | 3 | ||
共搬砖数 | 290 |
(2)问80名新团员中,男同学有多少人?