题目内容
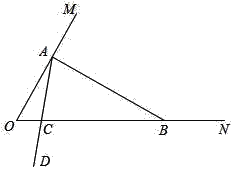
【题目】如图,等边△ABC的周长是12,D是AC边上的中点,点E在BC边的延长线上,如果DE=DB,那么CE的长是_______.

【答案】2
【解析】
由△ABC为等边三角形,且BD为边AC的中线,根据“三线合一”得到BD平分∠ABC,而∠ABC为60°,得到∠DBE为30°,又因为DE=DB,根据等边对等角得到∠E与∠DBE相等,故∠E也为30°;
由等边三角形的三边相等且周长为9,求出AC的长为3,且∠ACB为60°,根据∠ACB为△DCE的外角,根据三角形的外角等于与它不相邻的两个内角之和,求出∠CDE也为30°,根据等角对等边得到CD=CE,都等于边长AC的一半,从而求出CE的值.
∵△ABC为等边三角形,D为AC边上的中点,
∴BD为∠ABC的平分线,且∠ABC=60°,
即∠DBE=30°,又DE=DB,
∴∠E=∠DBE=30°,
∵等边△ABC的周长为9,
∴AC=3,且∠ACB=60°,
∴∠CDE=∠ACB∠E=30°,即∠CDE=∠E,
∴CD=CE=![]() AC=2.
AC=2.
故答案为:2.

【题目】某商场进行有奖促销活动,规定顾客购物达到一定金额就可以获得一次转动转盘的机会(如图),当转盘停止转动时指针落在哪一区域就可获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“10元兑换券”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
落在“10元兑换券”的频率 | 0.68 | a | 0.68 | 0.69 | b | 0.701 |
(1)a的值为 ,b的值为 ;
(2)假如你去转动该转盘一次,获得“10元兑换券”的概率约是 ;(结果精确到0.01)
(3)根据(2)的结果,在该转盘中表示“20元兑换券”区域的扇形的圆心角大约是多少度?(结果精确到1°)