��Ŀ����
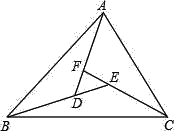
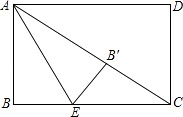
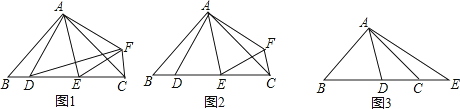
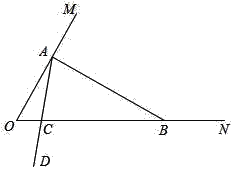
����Ŀ����һ���۽��������У����һ��������һ���ǵ�3�������������������dz�֮Ϊ���ǻ������������磬�����ڽǷֱ�Ϊ120�㣬40�㣬20���������������ǻ�������������ͼ����MON=60����������OM����һ��A������A��AB��OM��ON�ڵ�B����AΪ�˵�������AD��������OB�ڵ�C��
��1����ABO�Ķ���Ϊ_____�㣬��AOB_____���������������������� ���ǻ�����������
��2������OAC=20������֤����AOCΪ���ǻ�����������
��3������ABCΪ���ǻ���������ʱ�����OAC�Ķ�����
���𰸡���1��30���ǣ���2��֤������������3����OAC�Ķ���Ϊ80����52.5�㣮
��������
��1�����ݴ�ֱ�Ķ��塢�������ڽǺͶ��������ABO�Ķ������������ǻ����������ĸ����ж���
��2���������ǻ����������ĸ���֤��������
��3���֡�ABC=3��BAC����BCA=3��BAC����������������ǻ����������Ķ��������
��1����AB��OM�����OAB=90�㣬���ABO=90�㩁��MON=30�㣮
�ߡ�OAB=3��ABO�����AOBΪ���ǻ�����������
�ʴ�Ϊ��30������
��2����AOC=60�㣬��OAC=20�㣬���AOC=3��OAC�����AOCΪ���ǻ�����������
��3���ߡ�ABO=30�㣬���BAC+��BCA=150�㣮
�ߡ�ABCΪ���ǻ���������������ABC=3��BACʱ����BAC=10�㣬���OAC=90�㣭10��=80����
����BCA=3��BACʱ����BAC=37.5�㣬���OAC=90�㣭37.5��=52.5�㣮
����������ABCΪ���ǻ���������ʱ�����OAC�Ķ���Ϊ80����52.5�㣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�