Question

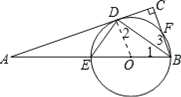
【题目】已知：如图，在Rt△ABC中，∠C=90°，BD平分∠ABC，交AC于点D，经过B、D两点的⊙O交AB 于点E，交BC于点F，EB为⊙O的直径．

（1）求证：AC是⊙O的切线；

（2）当BC=2，cos∠ABC=时，求⊙O的半径．

Answer 1

【答案】（1）见解析；（2）⊙O的半径为．

【解析】（1）连结OD，可证得OD∥BC，得到∠ADO=∠C=90°，从而得出结论；

（2）由cos∠ABC=，得到AB=6，由OD∥BC，得出△AOD∽△ABC，即可求出圆的半径．

（1）证明：如图，连结OD．

∴OD=OB．∴∠1=∠2．

∵BD平分∠ABC，∴∠1=∠3．

∴∠2=∠3．∴OD∥BC．

∴∠ADO=∠C=90°．∴OD⊥AC．

∵OD是⊙O的半径，

∴AC是⊙O的切线．

（2）解：在Rt△ACB中，∠C=90，BC=2，cos∠ABC=，

∴．

设⊙O的半径为r，则AO=6﹣r．

∵OD∥BC，

∴△AOD∽△ABC．

∴，∴．

解得．

∴⊙O的半径为．

“点睛”此题主要考查了切线的判定定理与相似三角形的判定和性质定理，此定理是初中阶段非常重要的定理，同学们应正确把握此定理．