题目内容
【题目】如图,在△ABC中,∠C=60°,∠A=40°.
(1)用尺规作图:作AB的垂直平分线,交AC于点D,交AB于点E(保留作图痕迹,不要求写作法和证明);
(2)求证:BD平分∠CBA.
【答案】
(1)解:如图①所示.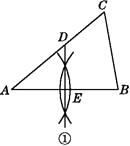
(2)解:证明:连接BD,如图②所示.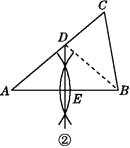
∵∠C=60°,∠A=40°,∴∠CBA=80°.
∵DE是AB的垂直平分线,∴AD=BD.
∴∠A=∠DBA=40°.
∴∠DBA= ![]() ∠CBA.
∠CBA.
∴BD平分∠CBA
【解析】(1)分别以A,B两点为圆心,以大于AB长度一半得长度为半径作弧,两弧在AB的两侧分别相交,过弧的两交点作直线,交AC于点D,交AB于点E,这条直线就是所求的AB的中垂线;
(2):连接BD,根据三角形的内角和得出∠CBA=80°,根据中垂线的性质得出AD=BD ,根据等边对等角得出∠A=∠DBA=40° ,从而得出∠DBA= ![]() ∠CBA,即BD平分∠CBA。
∠CBA,即BD平分∠CBA。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

