Question

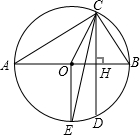
圆0的直径AB=15cm，弦CD=9cm，CF⊥CD交AB于F，DE⊥CD交AB于E，求四边形CDEF的面积．

Answer 1

过O作OM⊥CD于M，可得出M为CD的中点，连接OC，如图所示：
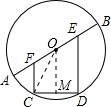∵FC⊥CD，ED⊥CD，
∴FC∥ED，又EF与CD相交，
∴四边形EFCD为直角梯形，
又CD=9cm，AB=15cm，
∴CM=

1

2

CD=4.5cm，
在Rt△OCM中，OC=

1

2

AB=7.5cm，CM=4.5cm，
根据勾股定理得：OM=

OC2-CM2

=6cm，
又M为CD中点，且FC∥OM∥ED，
∴O为EF的中点，即OM为梯形EFCD的中位线，
∴OM=

1

2

（FC+ED），即FC+ED=2OM=12cm，
则S_梯形EFCD=

1

2

CD（FC+ED）=

1

2

×9×12=54cm²．