题目内容
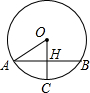
如图,AB为⊙O直径,C为圆上任一点,作弦CD⊥AB,垂足为H.连接OC.
(1)说明∠ACO=∠BCD成立的理由;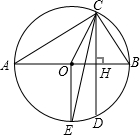
(2)作∠OCD的平分线CE交⊙O于E,连接OE(点D、E可以重合),求出点E在弧ADB的具体位置,并说明理由;
(3)在(2)的条件下,连接AE,判断圆上是否存在点C,使△ACE为等腰三角形?若存在,请你写出∠CAE的度数.(不用写出推理过程)
(1)说明∠ACO=∠BCD成立的理由;

(2)作∠OCD的平分线CE交⊙O于E,连接OE(点D、E可以重合),求出点E在弧ADB的具体位置,并说明理由;
(3)在(2)的条件下,连接AE,判断圆上是否存在点C,使△ACE为等腰三角形?若存在,请你写出∠CAE的度数.(不用写出推理过程)
(1)∵CD⊥直径AB,
∴弧BD=弧BC(垂径定理),
∴∠BCD=∠A,
∵OA=OC,
∴∠A=∠ACO,
∴∠ACO=∠BCD;
(2)E为弧ADB的中点.
理由:∵CE平分∠OCD,
∴∠OCE=∠DCE,
∵OE=OC,
∴∠OEC=∠OCE,
∴∠OEC=∠DCE,
∴OE∥CD,
又∵CD⊥AB∴OE⊥AB,
∴E为弧ADB的中点;
(3)当C在优弧ACE上,AC=CE时,∠CAE=67.5°,
当AC=AE时,∠CAE=90°,
当CE=AE时,∠CAE=45°,
当C在劣弧AE上,AC=CE时,∠CAE=22.5°.
∴弧BD=弧BC(垂径定理),
∴∠BCD=∠A,
∵OA=OC,
∴∠A=∠ACO,
∴∠ACO=∠BCD;
(2)E为弧ADB的中点.
理由:∵CE平分∠OCD,
∴∠OCE=∠DCE,
∵OE=OC,
∴∠OEC=∠OCE,
∴∠OEC=∠DCE,
∴OE∥CD,
又∵CD⊥AB∴OE⊥AB,
∴E为弧ADB的中点;
(3)当C在优弧ACE上,AC=CE时,∠CAE=67.5°,
当AC=AE时,∠CAE=90°,
当CE=AE时,∠CAE=45°,
当C在劣弧AE上,AC=CE时,∠CAE=22.5°.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目