Question

【题目】如图，菱形ABCD的边长为2cm，∠DAB=60°．点P从A点出发，以 cm/s的速度，沿AC向C作匀速运动；与此同时，点Q也从A点出发，以1cm/s的速度，沿射线AB作匀速运动．当P运动到C点时，P、Q都停止运动，设点P运动的时间为ts．
（1）点P由A点运动到C点需要秒；
（2）当P异于A、C时，请说明PQ∥BC；
（3）以P为圆心、PQ长为半径作圆，请问：在运动过程中，⊙P与边BC有2个公共点时t的取值范围？

Answer 1

【答案】
（1）2
（2）证明：连接BD交AC于点O．

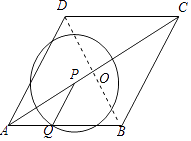
∵四边形ABCD是菱形，且边长为2cm，∠DAB=60°，

∴AB=BC=2，∠BAC= ∠BAD=30°，

∵AC⊥BD，OA= AC= ，

∴AC=2 ，∵AB=2，AP= t，AQ=t，

∴ = ．即 = ，又∵∠PAQ=∠CAB，

∴△PAQ≌△CAB，

∴∠APQ=∠ACB，

∴PQ∥BC．

（3）解：当⊙P与边BC 相切与点M时，连接PM，则PM⊥BC，

在Rt△CPM中，

∵∠PCM=30°，

∴PM= PC= ﹣ t，又PM=PQ=AQ=t，

即 ﹣ t=t，

∴t=4 ﹣6，

当⊙P过点B时，PQ=PB，

∵∠PQB=∠PAQ+∠APQ=60°，

∴△PQB为等边三角形，

∴QB=PQ=AQ=t，

∴t=1．

综上，若使⊙P与边BC有2个公共点，则4 ﹣6＜t≤1．

【解析】解：（1）由题意AC= ， ∴t= =2s，
所以答案是2．