题目内容
【题目】如图所示，已知等边△ABC的边长为a，P是△ABC内一点，PD∥AB，PE∥BC，PF∥AC，点D、E、F分别在BC、AC、AB上，猜想：PD+PE+PF等于多少，并证明你的猜想．
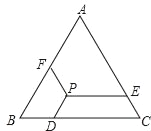
【答案】PD+PE+PF=a．理由见解析.
【解析】
延长EP交AB于G，延长FP交BC于H，然后证明△PFG和△PDH是等边三角形，根据等边三角形的性质求出PF=PG，PD=DH，再证明四边形BDPG和四边形CEPH是平行四边形，根据平行四边形的对边相等可得PG=BD，PE=CH，从而求出PD+PE+PF=BC．
解：PD+PE+PF=a．理由如下：
如图，延长EP交AB于G，延长FP交BC于H，
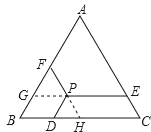
∵PE∥BC，PF∥AC，△ABC是等边三角形，
∴∠PGF=∠B=60°，∠PFG=∠A=60°，
∴△PFG是等边三角形，
同理可得△PDH是等边三角形，
∴PF=PG，PD=DH，
又∵PD∥AB，PE∥BC，
∴四边形BDPG是平行四边形，
∴PG=BD，
∴PD+PE+PF=DH+CH+BD=BC=a．
练习册系列答案
相关题目
