Question

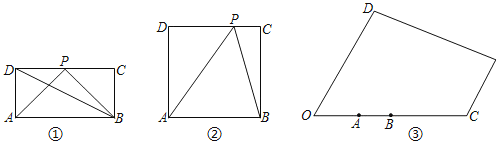
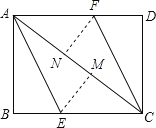
【题目】如图，AC为矩形ABCD的对角线，将边AB沿AE折叠，使点B落在AC上的点M处，将边CD沿CF折叠，使点D落在AC上的点N处．

(1)求证：四边形AECF是平行四边形；

(2)当AB与AC满足怎样数量关系时，四边形AECF为菱形．

Answer 1

【答案】（1）见解析；（2）,证明见解析

【解析】

（1）首先根据矩形与折叠的性质，通过“角边角”证明△ABE≌△CDF，则DF=BE，然后可得到AF=EC，依据一组对边平行且相等四边形是平行四边形即可证明AECF是平行四边形；

（2）若四边形AECF为菱形，则AE=CE，在Rt△ABC中利用折叠的性质可得∠BAE=∠CAE=∠ACB=30°，根据30°角所对直角边为斜边的一半可得.

（1）∵四边形ABCD为矩形，

∴AB=CD，AD∥BC，∠B=∠D=90°，∠BAC=∠DCA．

由翻折的性质可知：∠EAB=∠BAC，∠DCF=∠DCA，

∴∠EAB=∠DCF，

在△ABE和△CDF中

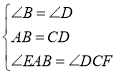
∴△ABE≌△CDF（ASA），

∴DF=BE，

∴AF=EC，

又∵AF∥EC，

∴四边形AECF是平行四边形；

（2）时，四边形AECF为菱形，

若四边形AECF为菱形，

∴AE=CE，

∴∠CAE=∠ACB，

∵∠BAE=∠CAE，

∴∠BAE=∠CAE=∠ACB=30°，

∴，

∴当时，四边形AECF为菱形.