题目内容
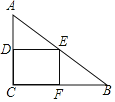
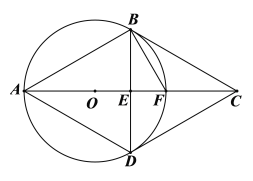
【题目】如图,菱形ABCD对角线交于点E,△ABD的外接圆⊙O交AC于点F.若FB=FC.
(1)证明:![]() =FEFA;
=FEFA;
(2)证明:BC是⊙O的切线;
(3)若EF=2,求出四边形ABCD的面积.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)首先根据菱形的性质和圆周角定理的推论得出△BEF∽△ABF,则有![]() ,即
,即![]() ,又因为FB=FC,则结论可证;
,又因为FB=FC,则结论可证;
(2)首先根据等腰三角形的性质和等量代换得出∠ABO=∠FBC,又因为∠ABO+∠FBO=∠ABF=90°,则有∠CBF+∠FBO =90°,进而可证明结论;
(3)首先根据三角形外角的性质和三角形内角和定理得出∠BAF=30°,∠BFA =60°,然后解直角三角形可求出AE,BE的长度,进而可求AC,BD的长度,最后利用菱形的面积公式即可求解.
(1)证明:∵四边形ABCD是菱形,
∴AC垂直平分BD,
∵AF为⊙O的直径.
∴∠ABF=90°.
![]() ,
,
∴△BEF∽△ABF.
∴![]() .
.
∴![]() .
.
∵FB=FC,
∴![]() =FEFA;
=FEFA;
(2)证明:连接OB,

∵OB=OA,FB=FC,BA=BC,
∴∠OBA=∠BAC,∠FBC=∠FCB,∠BAC=∠BCA.
∴∠ABO=∠FBC.
∵∠ABO+∠FBO=∠ABF=90°.
∴∠CBF+∠FBO =90°.
∴OB⊥BC.
∴BC是⊙O的切线;
(3)解:由(2)得∠BAC=∠BCA=∠FBC.
∴∠BFA=∠FBC+∠FCB=2∠FCB=2∠BAC.
∵∠BAF+∠BFA=180°-∠ABF=90°.
∴3∠BAF=90°.
∴∠BAF=30°.
∴∠BFA=2∠BAF=60°.
在Rt△BFE中,BE=EF![]() tan∠BFE=2
tan∠BFE=2![]() =
=![]() .
.
在Rt△BAE中,AE=![]() .
.
∴AC=2AE=12,BD=2BE=![]() .
.
∴四边形ABCD的面积S=![]() .
.

练习册系列答案
相关题目