Question

【题目】如图，小叶与小高欲测量公园内某棵树DE的高度．他们在这棵树正前方的一座楼亭前的台阶上的点A处测得这棵树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得这棵树顶端D的仰角为60°.已知点A的高度AB为3 m，台阶AC的坡度为1∶，且B，C，E三点在同一条直线上，那么这棵树DE的高度为(　　)

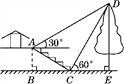
A. 6 m B. 7 m C. 8 m D. 9 m

Answer 1

【答案】D

【解析】过点A作AF⊥DE于点F，则四边形ABEF为矩形，

∴AF＝BE，EF＝AB＝3m．

设DE＝xm，在Rt△CDE中，CE＝＝xm．

在Rt△ABC中，∵＝，AB＝3m，

∴BC＝3m．

在Rt△AFD中，DF＝DE－EF＝(x－3) m，

∴AF＝＝ (x－3) m．

∵AF＝BE＝BC＋CE，

∴ (x－3)＝3＋x，

解得x＝9，

∴这棵树DE的高度为9m.

故选：D.