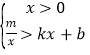题目内容
【题目】定义:我们把对角线互相垂直的四边形叫做神奇四边形.顺次连接四边形各边中点得到的四边形叫做中点四边形.
(1)判断:
①在平行四边形、矩形、菱形中,一定是神奇四边形的是 ;
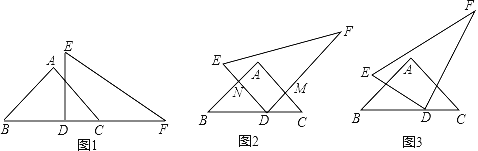
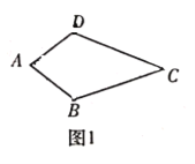
②命题:如图1,在四边形![]() 中,
中,![]() 则四边形
则四边形![]() 是神奇四边形.此命题是_____(填“真”或“假”)命题;
是神奇四边形.此命题是_____(填“真”或“假”)命题;
③神奇四边形的中点四边形是
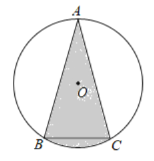
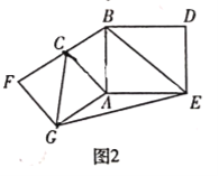
(2)如图2,分别以![]() 的直角边
的直角边![]() 和斜边
和斜边![]() 为边向外作正方形
为边向外作正方形![]() 和正方形
和正方形![]() ,连接
,连接![]()
①求证:四边形![]() 是神奇四边形;
是神奇四边形;
②若![]() ,求
,求![]() 的长;
的长;
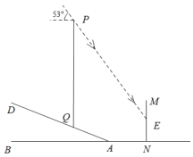
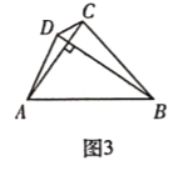
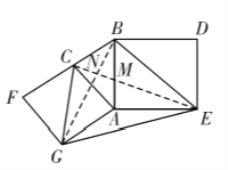
(3)如图3,四边形![]() 是神奇四边形,若
是神奇四边形,若![]() 分别是方程
分别是方程![]() 的两根,求
的两根,求![]() 的值.
的值.
【答案】(1)菱形;真;矩形;(2)①见解析,②![]() ;(3)5
;(3)5
【解析】
(1)①根据神奇四边形的定义即可判断;
②连接AC、BD,根据SSS证明△ADC≌△ABC得出∠DAC=∠BAC,再利用等腰三角形三线合一的性质证明AC⊥BD即可得到结论;
③根据四边形对角线互相垂直,运用三角形中位线平行于第三边证明四个角都是直角,判断是矩形.
(2)①判断出CE⊥BG,即可得出四边形BCGE是神奇四边形;
②利用勾股定理即得出![]() ,再把相关数据代入求解即可;
,再把相关数据代入求解即可;
(3)利用勾股定理即可得出![]() ,把
,把![]() ,
,![]() 代入求得
代入求得![]() ,再由方程
,再由方程![]() 得到
得到![]() ,
,![]() ,进而得出
,进而得出![]() ,求解方程即可.
,求解方程即可.
![]() ①∵在平行四边形、矩形、菱形中,两条对角线互相垂直的四边形是菱形,
①∵在平行四边形、矩形、菱形中,两条对角线互相垂直的四边形是菱形,
∴菱形一定是神奇四边形;
故答案为:菱形;
②连接AC、BD,
在△ACD和△ACB中,
∴△ACD≌△ACB
∴∠DAC=∠BAC
∵AB=AD
∴AC⊥BD
∴四边形![]() 是神奇四边形.
是神奇四边形.
故答案为:真;
③如图:∵E、F、G、H分别为各边中点,
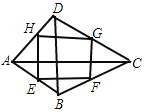
∴EF∥GH∥AC,EF=GH=![]() AC,
AC,
EH=FG=![]() DB,EH∥FG∥BD,
DB,EH∥FG∥BD,
∵DB⊥AC,
∴EF⊥EH,
∴四边形EFGH是矩形.
故答案为:矩形;
![]() 证明:连接
证明:连接![]() 相交于点
相交于点![]() 交
交![]() 于点
于点![]() ,如图所
,如图所
![]() 正方形
正方形![]() 和正方形
和正方形![]() ,
,
![]() ,
,
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,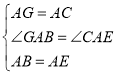
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即
,即![]()
![]() 四边形
四边形![]() 是神奇四边形;
是神奇四边形;
②![]() 四边形
四边形![]() 是神奇四边形,
是神奇四边形,
![]() ,
,
![]()
由勾股定理得![]()
![]() ,
,
![]() ,
,
![]()
![]()
![]() 正方形
正方形![]() 和正方形
和正方形![]() ,
,
![]() ,
,
![]() .
.
![]()
![]()
![]() 四边形
四边形![]() 是神奇四边形,同
是神奇四边形,同![]() 中②的证明方法,可得
中②的证明方法,可得![]()
![]()
![]()
![]()
又![]() 分别是方程
分别是方程![]() 的两根.
的两根.
![]()
![]()
解得![]()
当![]() 时,不合题意,所以舍去,
时,不合题意,所以舍去,
![]()

 名校课堂系列答案
名校课堂系列答案