ћвƒњƒЏ»Ё
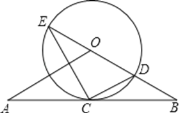
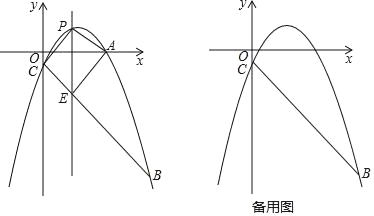
°Њћвƒњ°њ»зєы“їЄцЋƒ±я–ќµƒґ‘љ«ѕя∞—Ћƒ±я–ќЈ÷≥…ЅљЄц»эљ«–ќ£ђ“їЄц «µ»±я»эљ«–ќ£ђЅн“їЄц «Є√ґ‘љ«ѕяЋщґ‘µƒљ«ќ™![]() µƒ»эљ«–ќ£ђќ“√«∞—’вћхґ‘љ«ѕяљ–„ц’вЄцЋƒ±я–ќµƒјнѕлґ‘љ«ѕя£ђ’вЄцЋƒ±я–ќ≥∆ќ™јнѕлЋƒ±я–ќ£Ѓ
µƒ»эљ«–ќ£ђќ“√«∞—’вћхґ‘љ«ѕяљ–„ц’вЄцЋƒ±я–ќµƒјнѕлґ‘љ«ѕя£ђ’вЄцЋƒ±я–ќ≥∆ќ™јнѕлЋƒ±я–ќ£Ѓ
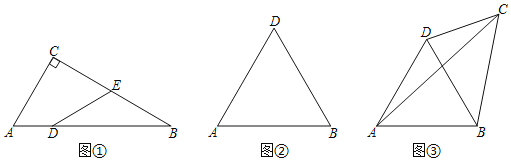
£®1£©»зЌЉҐў£ђ‘Џ![]() ÷–£ђ
÷–£ђ![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ![]() ќ™
ќ™![]() …ѕ“їµг£ђ
…ѕ“їµг£ђ![]() £ђ
£ђ![]() ќ™
ќ™![]() ÷–µг£ђЅђљ”
÷–µг£ђЅђљ”![]() £ђ«у÷§£ЇЋƒ±я–ќ
£ђ«у÷§£ЇЋƒ±я–ќ![]() ќ™јнѕлЋƒ±я–ќ£ї
ќ™јнѕлЋƒ±я–ќ£ї
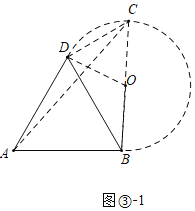
£®2£©»зЌЉҐЏ£ђ![]() «µ»±я»эљ«–ќ£ђ»ф
«µ»±я»эљ«–ќ£ђ»ф![]() ќ™јнѕлґ‘љ«ѕя£ђЋƒ±я–ќ
ќ™јнѕлґ‘љ«ѕя£ђЋƒ±я–ќ![]() ќ™јнѕлЋƒ±я–ќ£Ѓ«лї≠ЌЉ’“≥цЈыЇѕћхЉюµƒCµг¬д‘Џ‘х—щµƒЌЉ–ќ…ѕ£ї(‘ЏЌЉ÷–±к≥ц±Ў“™µƒ эЊЁ)
ќ™јнѕлЋƒ±я–ќ£Ѓ«лї≠ЌЉ’“≥цЈыЇѕћхЉюµƒCµг¬д‘Џ‘х—щµƒЌЉ–ќ…ѕ£ї(‘ЏЌЉ÷–±к≥ц±Ў“™µƒ эЊЁ)
£®3£©‘Џ£®2£©µƒћхЉюѕ¬£ђ
Ґў»ф![]() ќ™÷±љ«»эљ«–ќ£ђ
ќ™÷±љ«»эљ«–ќ£ђ![]() £ђ«у
£ђ«у![]() µƒ≥§ґ»£ї
µƒ≥§ґ»£ї
ҐЏ»зЌЉҐџ£ђ»ф![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ«л÷±љ”–і≥ц
£ђ«л÷±љ”–і≥ц![]() °Ґ
°Ґ![]() °Ґ
°Ґ![]() ÷ЃЉдµƒ эЅњєЎѕµ£Ѓ
÷ЃЉдµƒ эЅњєЎѕµ£Ѓ
°Њір∞Є°њ£®1£©ѕкЉыљвќц£ї£®2£©ѕкЉыљвќц£ї£®3£©Ґў![]() їт
їт![]() £ї ҐЏ
£ї ҐЏ![]()
°Њљвќц°њ
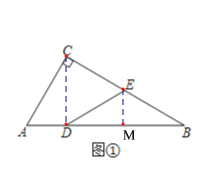
£®1£©Ѕђљ”CD£ђєэµгE„чEM°ЌAB£ђ“„÷§EM «BDµƒ÷–ієѕя£ђµ√°ѕEDB=°ѕB=30°г£ђі”ґшµ√°ѕCED=60°г£ђљшґшµ√![]() «µ»±я»эљ«–ќ£ђЉіњ…µ√µљљб¬џ£ї
«µ»±я»эљ«–ќ£ђЉіњ…µ√µљљб¬џ£ї
£®2£©„чµ»—ь»эљ«–ќODB£ђ єµ√OD£љOB£ђ°ѕDOB£љ120°г£ђ“‘Oќ™‘≤–ƒ£ђODќ™∞лЊґ„ч°—O£ђµ±µгC‘Џї°BCD…ѕ ±£ђ¬ъ„гћхЉю£ї
£®3£©Ґў»ф![]() ќ™÷±љ«»эљ«–ќ£ђЈ÷Ѕљ÷÷«йњцћ÷¬џ£Ї£®i£©µ±°ѕBDC=90°г ±£ї£®ii£©µ±°ѕDBC=90°г ±£ђЈ÷±р«у≥цір∞ЄЉіњ…£їҐЏљЂ
ќ™÷±љ«»эљ«–ќ£ђЈ÷Ѕљ÷÷«йњцћ÷¬џ£Ї£®i£©µ±°ѕBDC=90°г ±£ї£®ii£©µ±°ѕDBC=90°г ±£ђЈ÷±р«у≥цір∞ЄЉіњ…£їҐЏљЂ![]() »∆µгDƒж ±’л–э„™60°г£ђµ√µљ
»∆µгDƒж ±’л–э„™60°г£ђµ√µљ![]() £ђЅђљ”EC£ђєэµгE„чEF°ЌBC£ђљїBCµƒ—”≥§ѕя”ЏµгF£ђњ…µ√
£ђЅђљ”EC£ђєэµгE„чEF°ЌBC£ђљїBCµƒ—”≥§ѕя”ЏµгF£ђњ…µ√![]() «µ»±я»эљ«–ќ£ђ”√Їђx£ђyµƒіъ э љ±н ЊEF£ђCF£ђљшґшµ√µљBFµƒ±ніп љ£ђјы”√єіє…ґ®јн£ђЉіњ…µ√µљљб¬џ£Ѓ
«µ»±я»эљ«–ќ£ђ”√Їђx£ђyµƒіъ э љ±н ЊEF£ђCF£ђљшґшµ√µљBFµƒ±ніп љ£ђјы”√єіє…ґ®јн£ђЉіњ…µ√µљљб¬џ£Ѓ
£®1£©Ѕђљ”CD£ђєэµгE„чEM°ЌAB£ђ»зЌЉҐў£ђ
°я‘Џ![]() ÷–£ђ
÷–£ђ![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ
°аAB=4£ђBC=![]() £ђBD=4-1=3£ђ
£ђBD=4-1=3£ђ
°я![]() ќ™
ќ™![]() ÷–µг£ђ
÷–µг£ђ
°аBE=![]() £ђ
£ђ
°я‘Џ![]() ÷–£ђ°ѕB=30°г£ђEM°ЌAB£ђ
÷–£ђ°ѕB=30°г£ђEM°ЌAB£ђ
°аBM=BEcos30°г=![]() £ђ
£ђ
°аDM=BM=![]() £ђЉіEM «BDµƒ÷–ієѕя£ђ
£ђЉіEM «BDµƒ÷–ієѕя£ђ
°аED=EB=EC£ђ
°а°ѕEDB=°ѕB=30°г£ђ
°а°ѕCED=60°г£ђ
°а![]() «µ»±я»эљ«–ќ£ђ
«µ»±я»эљ«–ќ£ђ
”÷°я°ѕA=180°г-°ѕB-°ѕACB=60°г£ђ
°аЋƒ±я–ќ![]() ќ™јнѕлЋƒ±я–ќ£ї
ќ™јнѕлЋƒ±я–ќ£ї
£®2£©»зЌЉҐЏ÷–£ђ„чµ»—ь»эљ«–ќODB£ђ єµ√OD£љOB£ђ°ѕDOB£љ120°г£ђ“‘Oќ™‘≤–ƒ£ђODќ™∞лЊґ„ч°—O£ђµ±µгC‘Џї°BCD…ѕ ±£ђ°ѕDCB£љ![]() °ѕDOB£љ60°г£ђ¬ъ„гћхЉю£ї
°ѕDOB£љ60°г£ђ¬ъ„гћхЉю£ї
£®3£©Ґў»ф![]() ќ™÷±љ«»эљ«–ќ£ђЈ÷Ѕљ÷÷«йњцћ÷¬џ£Ї
ќ™÷±љ«»эљ«–ќ£ђЈ÷Ѕљ÷÷«йњцћ÷¬џ£Ї
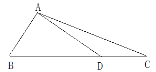
£®i£©µ±°ѕBDC=90°г ±£ђ»зЌЉҐџ-1£ђ
°я°ѕBCD=60°г£ђBC=2£ђ
°а°ѕDBC=30°г£ђBD=BC![]() cos30°г=
cos30°г=![]() £ђ
£ђ
°я![]() «µ»±я»эљ«–ќ£ђ
«µ»±я»эљ«–ќ£ђ
°аAB=BD=![]() £ђ°ѕABD=60°г£ђ
£ђ°ѕABD=60°г£ђ
°а°ѕABC=90°г£ђ
°а![]() £ї
£ї
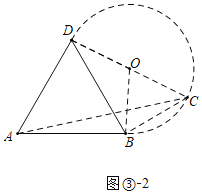
£®ii£©µ±°ѕDBC=90°г ±£ђ»зЌЉҐџ-2£ђ
Ќђјнњ…µ√£Ї°ѕADC=90°г£ђDC=4£ђAD=![]() £ђ
£ђ
°а![]() £Ѓ
£Ѓ
„џ…ѕЋщ ц£ЇAC=![]() їт
їт![]() £ї
£ї
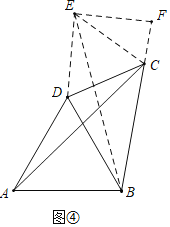
ҐЏљЂ![]() »∆µгDƒж ±’л–э„™60°г£ђµ√µљ
»∆µгDƒж ±’л–э„™60°г£ђµ√µљ![]() £ђЅђљ”EC£ђєэµгE„чEF°ЌBC£ђљїBCµƒ—”≥§ѕя”ЏµгF£ђ»зЌЉҐ№£ђ
£ђЅђљ”EC£ђєэµгE„чEF°ЌBC£ђљїBCµƒ—”≥§ѕя”ЏµгF£ђ»зЌЉҐ№£ђ
°а°ѕCDE=60°г£ђED=CD£ђBE=AC=z£ђ
°а![]() «µ»±я»эљ«–ќ£ђ
«µ»±я»эљ«–ќ£ђ
°аEC=CD=x£ђ°ѕDCE=60°г£ђ
°я°ѕBCD=60°г£ђ
°а°ѕECF=180°г-60°г-60°г=60°г£ђ
°аEF=EC![]() sin60°г=
sin60°г=![]() £ђCF= EC
£ђCF= EC![]() cos60°г=
cos60°г=![]() £ђ
£ђ
°аBF=BC+CF=y+![]() £ђ
£ђ
°аBE=![]() =
=![]() £ђ
£ђ
°аz=![]() £ђЉі£Ї
£ђЉі£Ї![]() £Ѓ
£Ѓ


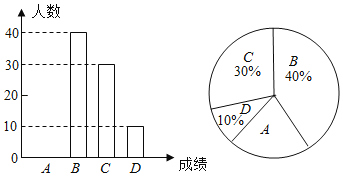
°Њћвƒњ°њќ™ЅЋљвƒ≥–£—І…ъґ‘°ґ„о«њіуƒ‘°Ј°Ґ°ґј ґЅ’я°Ј°Ґ°ґ÷–єъ Ђі іуїб°Ј°Ґ°ґ≥ц≤ ÷–єъ»Ћ°ЈЋƒЄцµз ”љЏƒњµƒѕ≤∞Ѓ«йњц£ђЋжЦi≥й»°ЅЋ![]() √ы—І…ъљш––µч≤йЌ≥Љ∆£®“™«у√њ√ы—І…ъ—°≥ц≤Ґ«“÷їƒ№—°≥ц“їЄц„‘ЉЇ„оѕ≤∞ЃµƒљЏƒњ£©£ђ≤ҐљЂµч≤йљбєыїж÷∆≥…»зЌЉЌ≥Љ∆ЌЉ±н£Ї
√ы—І…ъљш––µч≤йЌ≥Љ∆£®“™«у√њ√ы—І…ъ—°≥ц≤Ґ«“÷їƒ№—°≥ц“їЄц„‘ЉЇ„оѕ≤∞ЃµƒљЏƒњ£©£ђ≤ҐљЂµч≤йљбєыїж÷∆≥…»зЌЉЌ≥Љ∆ЌЉ±н£Ї
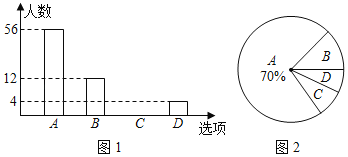
—І…ъ„оѕ≤∞ЃµƒљЏƒњ»Ћ эЌ≥Љ∆±н
љЏƒњ | »Ћ э£®√ы£© | ∞ўЈ÷±» |
„о«њіуƒ‘ | 5 | 10% |
ј ґЅ’я | 15 | |
÷–єъ Ђі іуїб |
| 40% |
≥ц≤ ÷–єъ»Ћ | 10 | 20% |
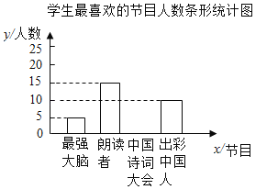
ЄщЊЁ“‘…ѕ–≈ѕҐ£ђїЎірѕ¬Ѕ–ќ ћв£Ї
£®1£©![]() °°£ђ
°°£ђ![]() °°£ї
°°£ї
£®2£©≤є»Ђ…ѕ√жµƒћх–ќЌ≥Љ∆ЌЉ£ї
£®3£©»фЄ√–£є≤”–—І…ъ![]() √ы£ђєјЉ∆Є√–£—І…ъ„оѕ≤∞Ѓ°ґј ґЅ’я°ЈљЏƒњµƒ»Ћ э£Ѓ
√ы£ђєјЉ∆Є√–£—І…ъ„оѕ≤∞Ѓ°ґј ґЅ’я°ЈљЏƒњµƒ»Ћ э£Ѓ