Question

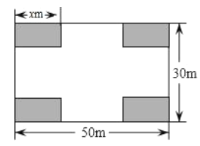
【题目】某社区决定把一块长，宽的矩形空地建成居民健身广场，设计方案如图，阴影区域为绿化区(四块绿化区为大小、形状都相同的矩形)，空白区域为活动区，且四周的4个出口宽度相同，其宽度不小于，不大于，设绿化区较长边为，活动区的面积为.为了想知道出口宽度的取值范围，小明同学根据出口宽度不小于，算出.

(1)求与的函数关系式并直接写出自变量的取值范围；

(2)求活动区的最大面积；

(3)预计活动区造价为50元/，绿化区造价为40元/，若社区的此项建造投资费用不得超过72000元，求投资费用最少时活动区的出口宽度？

Answer 1

【答案】(1)；(2)活动区的最大面积为；(3)投资最少时活动区的出口宽度为.

【解析】

（1）根据“活动区域的面积=矩形区域的面积-绿化区域的面积”可得y与x的关系式；

（2）根据二次函数的增减性可得结论；

（3）根据题意列方程即可得到结论．

(1)根据题意得，，

∴；

(2)，

∵，抛物线的开口向下，当时，随的增大而减小，

∴当时，，

答：活动区的最大面积为；

(3)设投资费用为元，

由题意得， ，

∴当时，解得：(不符合题意舍去)，，

∵，

∴当时，，

又∵，

∴.

∴当时，投资费用最少，此时出口宽度为，

答：投资最少时活动区的出口宽度为.