Question

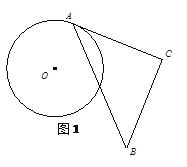
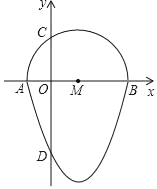
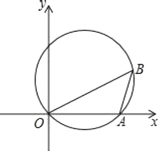
【题目】如图，已知点A（8，0），sin∠ABO＝，抛物线经过点O、A，且顶点在△AOB的外接圆上，则此抛物线的表达式为_____．

Answer 1

【答案】y＝﹣x2+4x或y＝x2﹣x.

【解析】

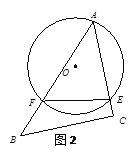
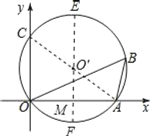
连接AC，过圆心O′作EF⊥OA，根据圆周角定理可得∠ABO＝∠OCA，从而求出直径AC=10，以及勾股定理和垂径定理得出E，F点着的坐标，进而分两种情况利用顶点式求出抛物线解析式即可．

解：如图所示：连接AC，过圆心O′作EF⊥OA，

∵∠AOC＝90°，∠ABO＝∠OCA，

∴ ，

∵点A（8，0），

∴AC＝10，

根据题意得出：AM＝OM＝4，AO′＝5，

∴MO′＝3，∴MF＝2，

∴F点坐标为：（4，﹣2），

设过O，A，F的抛物线解析式为：y＝a（x﹣4）2﹣2，

将A代入（8，0）得：0＝a（8﹣4）2﹣2，

解得：a＝，

∴此时抛物线解析式为：y＝（x﹣4）2﹣2＝x2﹣x，

根据题意得出：AM＝OM＝4，AO′＝5，

∴MO′＝3，∴ME＝8，

∴E点坐标为：（4，8），

设过O，A，E的抛物线解析式为：y＝a（x﹣4）2+8，

将A代入（8，0）得：

0＝a（8﹣4）2+8，

解得：a＝﹣，

∴此时抛物线解析式为：y＝﹣（x﹣4）2+8＝﹣x2+4x，

故答案是：y＝﹣x2+4x或y＝x2﹣x.