题目内容
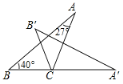
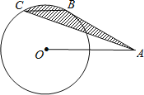
【题目】如图,A是半径为2的⊙O外的一点,OA=4,AB切⊙O于点B,弦BC∥OA,连接AC,则图中阴影部分的面积为___________
【答案】![]() π
π
【解析】
连接OB、OC,如图,利用切线的性质得∠ABO=90°,再利用直角三角形的性质可求出∠BAO=30°,则∠AOB=60°,接着利用平行线的性质得到∠CBO=∠AOB=60°,利用三角形面积公式可得到S△ABC=S△OCB,然后根据扇形的面积公式,利用图中阴影部分的面积=S扇形BOC进行计算.
解:连接OB、OC,如图,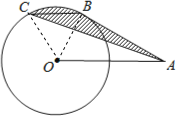
∵AB切⊙O于点B,
∴OB⊥AB,
∴∠ABO=90°,
在Rt△ABO中,∵OA=4,OB=2,
∴∠BAO=30°,
∴∠AOB=60°,
∵BC∥OA,
∴∠CBO=∠AOB=60°,S△ABC=S△OCB,
∴∠BOC=60°,图中阴影部分的面积=S扇形BOC,
∴图中阴影部分的面积=![]() =
=![]() π.
π.
故答案为![]() π.
π.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目