Question

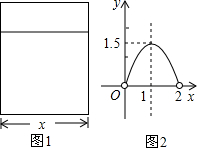
用铝合金型材做一个形状如图1所示的矩形窗框，设窗框的一边为xm．窗户的适光面积为ym²，y与x的函数图象如图2所示．
（1）当窗户透光面积最大时，求窗框的两边长；
（2）要使窗户透光面积不小于1m²．则窗框的一边长x应该在什么范围内取值？

Answer 1

（1）由图象可知，当x=l时，透光面积y=1.5最大．
设此时窗框的另一边长为z，则y=zx，
将x=1，y=1.5代入得z=1.5，
故可得窗框的一边长为1m．另一边是1.5m；

（2）由已知可设二次函数关系式为y=a（x-1）²+1.5，
将（0，0）代入，可得：0=a+1.5，
解得：a=-1.5，
则该二次函数的关系式为：y=-1.5（x-l）²+1.5，
由y=1得：-1.5（x-1）²+1.5=1，
解得x₁=1-

3

3

，x₂=1+

3

3

，
由图象可知，当1-

3

3

≤x≤1+

3

3

时，窗户透光面积不小于lm²．