ÌâÄ¿ÄÚÈÝ
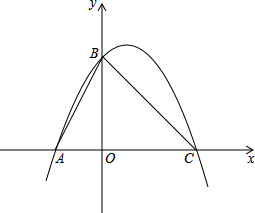
Èçͼ£¬ÔÚƽÃæÖ±½Ç×ø±êϵÖУ¬Å×ÎïÏßy=-
x2+bx+c¾¹ýA£¨-2£¬0£©£¬C£¨4£¬0£©Á½µã£¬ºÍyÖáÏཻÓÚµãB£¬Á¬½ÓAB¡¢BC£®
£¨1£©ÇóÅ×ÎïÏߵĽâÎöʽ£¨¹Øϵʽ£©£®
£¨2£©ÔÚµÚÒ»ÏóÏÞÍ⣬ÊÇ·ñ´æÔÚµãE£¬Ê¹µÃÒÔBCΪֱ½Ç±ßµÄ¡÷BCEºÍRt¡÷AOBÏàËÆ£¿Èô´æÔÚ£¬Çë¼òҪ˵Ã÷ÈçºÎÕÒµ½·ûºÏÌõ¼þµÄµãE£¬È»ºóÖ±½Óд³öµãEµÄ×ø±ê£¬²¢ÅжÏÊÇ·ñÓÐÂú×ãÌõ¼þµÄµãEÔÚÅ×ÎïÏßÉÏ£»Èô²»´æÔÚ£¬Çë˵Ã÷ÀíÓÉ£®
£¨3£©ÔÚÖ±ÏßBCÉÏ·½µÄÅ×ÎïÏßÉÏ£¬ÕÒÒ»µãD£¬Ê¹S¡÷BCD£ºS¡÷ABC=1£º4£¬²¢Çó³ö´ËʱµãDµÄ×ø±ê£®
| 1 |
| 2 |
£¨1£©ÇóÅ×ÎïÏߵĽâÎöʽ£¨¹Øϵʽ£©£®
£¨2£©ÔÚµÚÒ»ÏóÏÞÍ⣬ÊÇ·ñ´æÔÚµãE£¬Ê¹µÃÒÔBCΪֱ½Ç±ßµÄ¡÷BCEºÍRt¡÷AOBÏàËÆ£¿Èô´æÔÚ£¬Çë¼òҪ˵Ã÷ÈçºÎÕÒµ½·ûºÏÌõ¼þµÄµãE£¬È»ºóÖ±½Óд³öµãEµÄ×ø±ê£¬²¢ÅжÏÊÇ·ñÓÐÂú×ãÌõ¼þµÄµãEÔÚÅ×ÎïÏßÉÏ£»Èô²»´æÔÚ£¬Çë˵Ã÷ÀíÓÉ£®
£¨3£©ÔÚÖ±ÏßBCÉÏ·½µÄÅ×ÎïÏßÉÏ£¬ÕÒÒ»µãD£¬Ê¹S¡÷BCD£ºS¡÷ABC=1£º4£¬²¢Çó³ö´ËʱµãDµÄ×ø±ê£®

£¨1£©¡ßÅ×ÎïÏßy=-
x2+bx+c¾¹ýA£¨-2£¬0£©£¬C£¨4£¬0£©Á½µã£¬
¡à
£¬
½âµÃ
£®
¡àÅ×ÎïÏߵĽâÎöʽΪy=-
x2+x+4£®
£¨2£©ÔÚµÚÒ»ÏóÏÞÍâ´æÔÚµãE£¬Ê¹µÃÒÔBCΪֱ½Ç±ßµÄ¡÷BCEºÍRt¡÷AOBÏàËÆ£®
µ±BCΪֱ½Ç±ßʱ£¬
ÈôµãBΪֱ½Ç¶¥µã£¬ÔòµãEµÄ×ø±êΪ£¨-8£¬-4£©£¬´ËʱµãE²»ÔÚÅ×ÎïÏßÉÏ£»
ÈôµãCΪֱ½Ç¶¥µã£¬ÔòµãEµÄ×ø±êΪ£¨-4£¬-8£©£¬´ËʱµãEÔÚÅ×ÎïÏßÉÏ£®
£¨3£©¡ßS¡÷ABC=
¡Á6¡Á4=12£¬S¡÷BCD£ºS¡÷ABC=1£º4£¬
¡àS¡÷BCD=
S¡÷ABC=
¡Á12=3£®
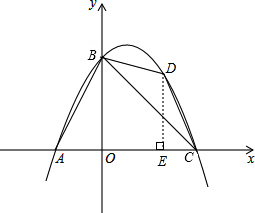
ÈçͼËùʾ£¬ÉèÔÚÖ±ÏßBCÉÏ·½µÄÅ×ÎïÏßÉÏ£¬ÕÒÒ»µãDµÄ×ø±êΪ£¨x£¬-
x2+x+4£©£¬×÷DE¡ÍxÖáÓÚµãE£¬Ôò
S¡÷BCD=SÌÝÐÎBOED+S¡÷DCE-S¡÷BOC
=
¡Á(-
x2+x+4+4)¡Áx+
¡Á(4-x)¡Á(-
x2+x+4)-
¡Á4¡Á4=3£®
¼´x2-4x+3=0£¬
½âµÃx1=1£¬x2=3£®
¡àµãDµÄ×ø±êΪ£¨1£¬
£©»ò£¨3£¬
£©£®
| 1 |
| 2 |
¡à
|
½âµÃ
|
¡àÅ×ÎïÏߵĽâÎöʽΪy=-
| 1 |
| 2 |
£¨2£©ÔÚµÚÒ»ÏóÏÞÍâ´æÔÚµãE£¬Ê¹µÃÒÔBCΪֱ½Ç±ßµÄ¡÷BCEºÍRt¡÷AOBÏàËÆ£®
µ±BCΪֱ½Ç±ßʱ£¬
ÈôµãBΪֱ½Ç¶¥µã£¬ÔòµãEµÄ×ø±êΪ£¨-8£¬-4£©£¬´ËʱµãE²»ÔÚÅ×ÎïÏßÉÏ£»
ÈôµãCΪֱ½Ç¶¥µã£¬ÔòµãEµÄ×ø±êΪ£¨-4£¬-8£©£¬´ËʱµãEÔÚÅ×ÎïÏßÉÏ£®
£¨3£©¡ßS¡÷ABC=
| 1 |
| 2 |
¡àS¡÷BCD=
| 1 |
| 4 |
| 1 |
| 4 |
ÈçͼËùʾ£¬ÉèÔÚÖ±ÏßBCÉÏ·½µÄÅ×ÎïÏßÉÏ£¬ÕÒÒ»µãDµÄ×ø±êΪ£¨x£¬-
| 1 |
| 2 |
S¡÷BCD=SÌÝÐÎBOED+S¡÷DCE-S¡÷BOC
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
¼´x2-4x+3=0£¬
½âµÃx1=1£¬x2=3£®
¡àµãDµÄ×ø±êΪ£¨1£¬
| 9 |
| 2 |
| 5 |
| 2 |


Á·Ï°²áϵÁдð°¸
 ÌìÌìÏòÉÏÒ»±¾ºÃ¾íϵÁдð°¸
ÌìÌìÏòÉÏÒ»±¾ºÃ¾íϵÁдð°¸ СѧÉú10·ÖÖÓÓ¦ÓÃÌâϵÁдð°¸
СѧÉú10·ÖÖÓÓ¦ÓÃÌâϵÁдð°¸
Ïà¹ØÌâÄ¿
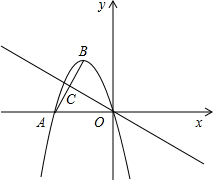 BÖе㣬µãEÊÇÖ±ÏßOCÉϵÄÒ»¸ö¶¯µã£¨µãEÓëµãO²»Öغϣ©£¬µãDÔÚyÖáÉÏ£¬ÇÒEO=ED£®
BÖе㣬µãEÊÇÖ±ÏßOCÉϵÄÒ»¸ö¶¯µã£¨µãEÓëµãO²»Öغϣ©£¬µãDÔÚyÖáÉÏ£¬ÇÒEO=ED£®
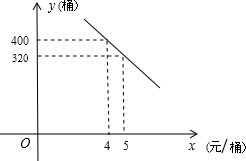 £¿£¨²»³¬¹ý30×Ö£©
£¿£¨²»³¬¹ý30×Ö£©
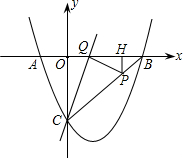
 ¶ÎPCÓÚE£¬ÇÒPD=PE£®
¶ÎPCÓÚE£¬ÇÒPD=PE£®